순차 탐색(Sequential Search)
리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법
- 가장 기본 탐색 방법
- 구현이 간단
- count() 메소드 등에도 내부에서 순차 탐색 수행
- 데이터 개수가 N개일 때 최대 N번의 비교 연산 → 최악의 경우 시간 복잡도 O(N)
코드 구현
# 순차 탐색 소스코드
def sequential_search(n, target, array):
# 각 원소를 하나씩 확인하며
for i in range(n):
# 현재의 원소가 찾고자 하는 원소와 동일한 경우
if array[i] == target:
return i + 1 # 현재의 위치 반환(인덱스는 0부터 시작하므로 1 더하기)
이진 탐색(Binary Search)
찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 데이터 찾는 방법
- 탐색 범위를 절반씩 좁혀가며 데이터 탐색
- 데이터가 무작위일 때는 사용할 수 없지만, 이미 정렬되어 있다면 매우 빠르게 데이터 찾을 수 있음
- 위치 변수 3개(시작점, 중간점, 끝점) 사용
- 한 번 확인할 때마다 원소의 개수 절반씩 줄어듦 → 시간 복잡도 O(logN)
(단계마다 2로 나누는 것과 동일)


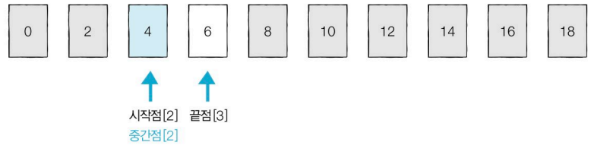
전체 데이터의 개수는 10개지만, 이진 탐색을 통해 총 3번의 탐색으로 원소 발견
데이터와 중간점을 비교해서
ㄴ 데이터 > 중간점 : 중간점=시작점, 중간점=(끝점-시작점)//2 → 오른쪽에 존재
ㄴ 데이터 == 중간점 : 데이터 = 중간점
ㄴ 데이터 < 중간점 : 중간점=끝점, 중간점=(끝점-시작점)//2 → 왼쪽에 존재
코드
< 재귀 함수 ver. >
# 재귀 함수로 구현한 이진 탐색 소스코드
def binary_search(array, target, start, end):
if start > end:
return None
mid = (start + end) // 2
# 찾은 경우 중간점 인덱스 반환
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
elif array[mid] > target:
return binary_search(array, target, start, mid - 1)
# 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else:
return binary_search(array, target, mid + 1, end)
* 몫 연산자(//)와 int( ) 함수 모두 나눈 몫을 구하는 코드
< 반복문 ver. >
# 반복문으로 구현한 이진 탐색 소스코드
def binary_search(array, target, start, end):
while start <= end:
mid = (start + end) // 2
# 찾은 경우 중간점 인덱스 반환
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 : 왼쪽 확인
elif array[mid] > target:
end = mid - 1
# 중간점의 값보다 찾고자 하는 값이 큰 경우 : 오른쪽 확인
else:
start = mid + 1
return None
코딩테스트에서...
- 이진 탐색의 소스코드를 구현하는 것은 상당히 어려운 작업이 될 수 있음, 자연스럽게 꼭 외우자!!!
이 원리는 다른 알고리즘에서도 폭넓게 적용되는 원리와 유사하기 때문에 매우 중요 - 코테의 이진 탐색 문제는 탐색 범위가 큰 상황에서 탐색을 가정하는 문제가 많음
탐색 범위가 2,000만을 넘어가면 이진 탐색으로 문제에 접근 - 처리 데이터 개수나 값이 1,000만 단위 이상으로 넘어가면 O(logN) 속도 내야하는 경우
트리 자료구조
- DB는 내부적으로 대용량 데이터 처리에 적합한 트리 자료구조를 이용하여 데이터 항상 정렬
- 이진 탐색과 유사한 방법을 이용해 탐색을 항상 빠르게 수행하도록 설계, 빠름
- 트리 자료구조는 그래프 자료구조의 일종, DB 시스템이나 파일 시스템에서 많은 데이터 관리를 위한 목적으로 사용
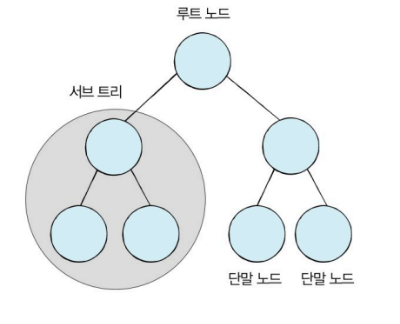
트리 자료구조 특징
- 부모 노드와 자식 노드의 관계로 표현
- 최상단 노드 = 루트 노드
- 최하단 노드 = 단말 노드
- 트리의 일부를 떼어내도 트리 구조 = 서브 트리
- 파일 시스템과 같이 계층적이고 정렬된 데이터 다루기에 적합
이진 탐색 트리
이진 탐색이 동작할 수 있도록 고안된, 효율적인 탐색이 가능한 자료구조

이진 탐색 트리 특징
- 부모 노드보다 왼쪽 자식 노드가 작다
- 부모 노드보다 오른쪽 자식 노드가 크다
- 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드
*구현 요구하는 문제는 출제 빈도 낮음

빠르게 입력받기
- 이진 탐색 문제는 입력 데이터가 많거나, 탐색 범위가 매우 넓은 편
→ 데이터 1,000만 개 넘거나, 탐색 범위 크기 1,000억 이상이라면 이진 탐색 알고리즘 의심 - input( ) 함수 사용하면 동작 속도 느려서 시간 초과
- 입력 데이터 많은 문제 : sys 라이브러리의 readline( ) 함수로 시간 초과 피하기
코드
# 한 줄 입력받아 출력하는 소스코드
import sys
# 하나의 문자열 데이터 입력받기
input_data = sys.stdin.readline().rstrip()
# 입력받은 문자열 그대로 출력
print(input_data)*한 줄 입력받고 rstrip( ) 함수 꼭 호출
→ readline() 은 입력 후 엔터가 줄 바꿈 기호로 입력됨, 이 공백 문자 제거. 관행적으로 암기!
'Programming > 알고리즘 & 코테' 카테고리의 다른 글
| [이진 탐색] 떡볶이 떡 만들기 (실전문제, 이것이 코딩테스트다 with 파이썬) (0) | 2023.12.27 |
|---|---|
| [이진 탐색] 부품 찾기 (실전문제, 이것이 코딩테스트다 with 파이썬) (0) | 2023.12.26 |
| [정렬] 두 배열의 원소 교체 (실전문제, 이것이 코딩테스트다 with 파이썬) (2) | 2023.12.26 |
| [정렬] 성적이 낮은 순서로 학생 출력하기 (실전문제, 이것이 코딩테스트다 with 파이썬) (0) | 2023.12.26 |
| [정렬] 위에서 아래로 (실전문제, 이것이 코딩테스트다 with 파이썬) (1) | 2023.12.26 |
