Math/선형대수

2장 넘파이(Numpy)로 공부하는 선형대수

kk_______yy 2024. 3. 15. 18:03

2.1 데이터와 행렬

2.2 벡터와 행렬의 연산

2.3 행렬의 성질

2.4 선형 연립방정식과 역행렬

2.1 데이터와 행렬

데이터 유형

스칼라 : 숫자 하나
벡터 : 여러 숫자로 이루어진 데이터 레코드
행렬 : 벡터, 즉 데이터 레코드가 여럿인 데이터 집합
텐서 : 같은 크기의 행렬이 여러 개 있는 것

벡터

복수의 가로줄(행), 하나의 세로줄(열) = 열벡터
볼드체 벡터 기호, 화살표 벡터 기호(데이터 사이언스 분야에서는 굳이 기호 사용하지 않기도)
특징벡터 : 예측 문제에서 입력 데이터로 사용되는 데이터 벡터

벡터를 넘파이로 표현

열 개수가 하나인 2차원 배열 객체
* 배열의 차원 != 벡터의 차원(원소 개수)
넘파이는 1차원 배열 객체도 대부분 벡터로 인정(행처럼 표시되어도 실제로는 열)

x1 = np.array([[5.1], [3.5], [1.4], [0.2]])
x1
# 실행 결과
array([[5.1],
       [3.5],
       [1.4],
       [0.2]])
       
x1 = np.array([5.1, 3.5, 1.4, 0.2])
x1
# 실행 결과
array([5.1, 3.5, 1.4, 0.2])

예측 문제의 입력 데이터는 대부분 벡터로 표시
이미지는 원래 2차원 데이터이지만 에측 문제에서는 보통 1차원 벡터로 변환하여 사용

행렬

행렬은 보통 X와 같이 알파벳 대문자로 표기
[ x2,3 ] 처럼 두 숫자 쌍을 아래첨자로 붙여서 표기
- 첫 번째 숫자 : 행
- 두 번째 숫자 : 열
데이터를 행렬로 묶어서 표시할 때는, 하나의 벡터라 '행'으로 표시
즉, 단독 벡터는 열벡터, 복수의 벡터는 여러 행벡터로 표기
스칼라와 벡터도 수학적으로는 행렬

텐서

같은 크기의 행렬이 여러 개 같이 묶여 있는 것
ex)컬러 이미지는 2차원의 행렬로 보이지만, 사실 R, G, B의 밝기를 나타내는 3가지 이미지가 겹친 것
- 채널 : 각각의 색을 나타내는 행렬

from scipy import misc  # 패키지 임포트

img_rgb = misc.face()  # 컬러 이미지 로드
img_rgb.shape  # 데이터의 모양 : (768, 1024, 3)

plt.subplot(221)
plt.imshow(img_rgb, cmap=plt.cm.gray)  # 컬러 이미지 출력
plt.axis("off")
plt.title("RGB 컬러 이미지")

plt.subplot(222)
plt.imshow(img_rgb[:, :, 0], cmap=plt.cm.gray)  # red 채널 출력
plt.axis("off")
plt.title("Red 채널")

plt.subplot(223)
plt.imshow(img_rgb[:, :, 1], cmap=plt.cm.gray)  # green 채널 출력
plt.axis("off")
plt.title("Green 채널")

plt.subplot(224)
plt.imshow(img_rgb[:, :, 2], cmap=plt.cm.gray)  # blue 채널 출력
plt.axis("off")
plt.title("Blue 채널")

plt.show()

전치 연산

행렬의 행과 열을 바꾸는 연산
벡터나 행렬에 T라는 위첨자를 붙여서 표기 ( ' 를 붙이기도 함)
전치 연산으로 만든 행렬을 원래 행렬에 대한 전치행렬이라 함

A = np.array([[11,12,13],[21,22,23]])
A
array([[11, 12, 13],
       [21, 22, 23]])

# 전치 연산
A.T    # 메서드가 아닌 속성이므로 () 없이 호출
array([[11, 21],
       [12, 22],
       [13, 23]])

열벡터 x에 대한 전치행렬은 행벡터가 됨
(다만 1차원 ndarray는 전치 연산이 정의되지 않음)

특수한 벡터와 행렬

영벡터 : 모든 원소가 0인 N차원 벡터, zeros( )
일벡터 : 모든 원소가 1인 n차원 벡터, ones( )
정방행렬 : 행 개수와 열 개수가 같은 행렬
대각행렬 : 모든 비대각 요소가 0인 행렬, diag( )
- 대각(주 대각) : 행렬에서 행과 열이 같은 위치
- 비대각 : 대각 위치에 있지 않은 것들
항등행터 : 모든 대각성분의 값이 1인 대각행렬, identity( ) or eye( )
대칭행렬 : 전치연산을 통해 얻은 전치행렬과 원래의 행렬이 같은 행렬

2.2 벡터와 행렬의 연산

요소별 연산

같은 크기를 가진 두 개의 벡터나 행렬은 덧셈과 뺄셈을 할 수 있음

x = np.array([10, 11, 12, 13, 14])
y = np.array([0, 1, 2, 3, 4])
x + y
>>> array([10, 12, 14, 16, 18])
x - y
>>> array([10, 10, 10, 10, 10])

스칼라와 벡터/행렬의 곱셈

벡터 x 또는 행렬 A의 모든 원소에 스칼라값 c를 곱하는 것

브로드캐스팅

벡터와 스칼라의 경우에 스칼라를 벡터로 변환한 연산 허용

선형조합

벡터/행렬에 스칼라값을 곱한 후 더하거나 뺀 것

내적

두 벡터의 차원(길이)이 같아야 함
앞의 벡터가 행벡터이고 뒤의 벡터가 열벡터여야 함

x = np.array([[1], [2], [3]])
y = np.array([[4], [5], [6]])

x.T @ y  # 또는 np.dot(x.T, y)
>>> array([[32]])


x = np.array([1, 2, 3])
y = np.array([4, 5, 6])

x @ y  # 또는 np.dot(x, y)
>>> 32

가중합

복수의 데이터 각각에 어떤 가중치를 곱한 후 이 곱셈 결과들을 다시 합한 것

가중평균

가중합의 가중치값을 전체 가중치값의 합으로 나눈 것
ex) 대학교 평균 성적
mean( ) 메서드 사용

유사도

두 벡터가 닮은 정도를 정량적으로 나타낸 값
두 벡터가 비슷한 경우 유사도가 커지고, 아닌 경우 유사도 작아짐
내적 이용하면 '코사인 유사도'를 계산할 수 있음
- 동일 이미지의 내적값이 비교적 더 크다

# 0과 1을 나타내는 MNIST 이미지에 대한 내적
from sklearn.datasets import load_digits
import matplotlib.gridspec as gridspec

digits = load_digits()
d1 = digits.images[0]
d2 = digits.images[10]
d3 = digits.images[1]
d4 = digits.images[11]
v1 = d1.reshape(64, 1)
v2 = d2.reshape(64, 1)
v3 = d3.reshape(64, 1)
v4 = d4.reshape(64, 1)

plt.figure(figsize=(9, 9))
gs = gridspec.GridSpec(1, 8, height_ratios=[1],
                       width_ratios=[9, 1, 9, 1, 9, 1, 9, 1])
for i in range(4):
    plt.subplot(gs[2 * i])
    plt.imshow(eval("d" + str(i + 1)), aspect=1,
               interpolation='nearest', cmap=plt.cm.bone_r)
    plt.grid(False)
    plt.xticks([])
    plt.yticks([])
    plt.title("image {}".format(i + 1))
    plt.subplot(gs[2 * i + 1])
    plt.imshow(eval("v" + str(i + 1)), aspect=0.25,
               interpolation='nearest', cmap=plt.cm.bone_r)
    plt.grid(False)
    plt.xticks([])
    plt.yticks([])
    plt.title("vector {}".format(i + 1))
plt.tight_layout()
plt.show()

# 0과 0 이미지, 1과 1 이미지의 내적값
(v1.T @ v2)[0][0], (v3.T @ v4)[0][0]
>>> (3064.0, 3661.0)

# 0과 1 이미지, 1과 0 이미지의 내적값
(v1.T @ v3)[0][0], (v1.T @ v4)[0][0], (v2.T @ v3)[0][0], (v2.T @ v4)[0][0]
>>> (1866.0, 1883.0, 2421.0, 2479.0)

선형회귀 모형

독립변수 x에서 종속변수 y를 예측하는 방법의 하나
독립 변수 벡터 x와 가중치 벡터 w와 의 가중합으로 y에 대한 예측값 y^를 계산하는 수식
가장 단순하면서도 가장 널리 쓰이는 예측 모델
ex) 단지 내 아파트 가격 예측 모형
- 면적 x1, 층수 x2, 한강 보이는 여부 x3, 아파트 예측 가격 y^
단점 : 비선형적인 현실 세계의 데이터 잘 예측하지 못할 수 있음
→ 선형회귀 모형을 수정한 모델 사용

제곱합

데이터의 분산이나 표준 편차 등을 구하는 경우에 각각의 데이터를 제곱한 뒤 이 값을 모두 더한 것
벡터의 내적을 사용하여 xT·x로 쓸 수 있음

행렬과 행렬의 곱셈

@ 또는 dot( ) 명령

A = np.array([[1, 2, 3], [4, 5, 6]])
B = np.array([[1, 2], [3, 4], [5, 6]])
C = A @ B
C
array([[22, 28],
       [49, 64]])

교환 법칙과 분배 법칙

곱셈의 연결

항등행렬의 곱셈

열벡터의 선형조합

ex) 두 이미지 벡터의 선형조합은 두 이미지를 섞어놓은 모핑 효과에 사용

from sklearn.datasets import fetch_olivetti_faces

faces = fetch_olivetti_faces()

f, ax = plt.subplots(1, 3)

ax[0].imshow(faces.images[6], cmap=plt.cm.bone)
ax[0].grid(False)
ax[0].set_xticks([])
ax[0].set_yticks([])
ax[0].set_title("image 1: $x_1$")

ax[1].imshow(faces.images[10], cmap=plt.cm.bone)
ax[1].grid(False)
ax[1].set_xticks([])
ax[1].set_yticks([])
ax[1].set_title("image 2: $x_2$")

new_face = 0.7 * faces.images[6] + 0.3 * faces.images[10]
ax[2].imshow(new_face, cmap=plt.cm.bone)
ax[2].grid(False)
ax[2].set_xticks([])
ax[2].set_yticks([])
ax[2].set_title("image 3: $0.7x_1 + 0.3x_2$")

plt.show()

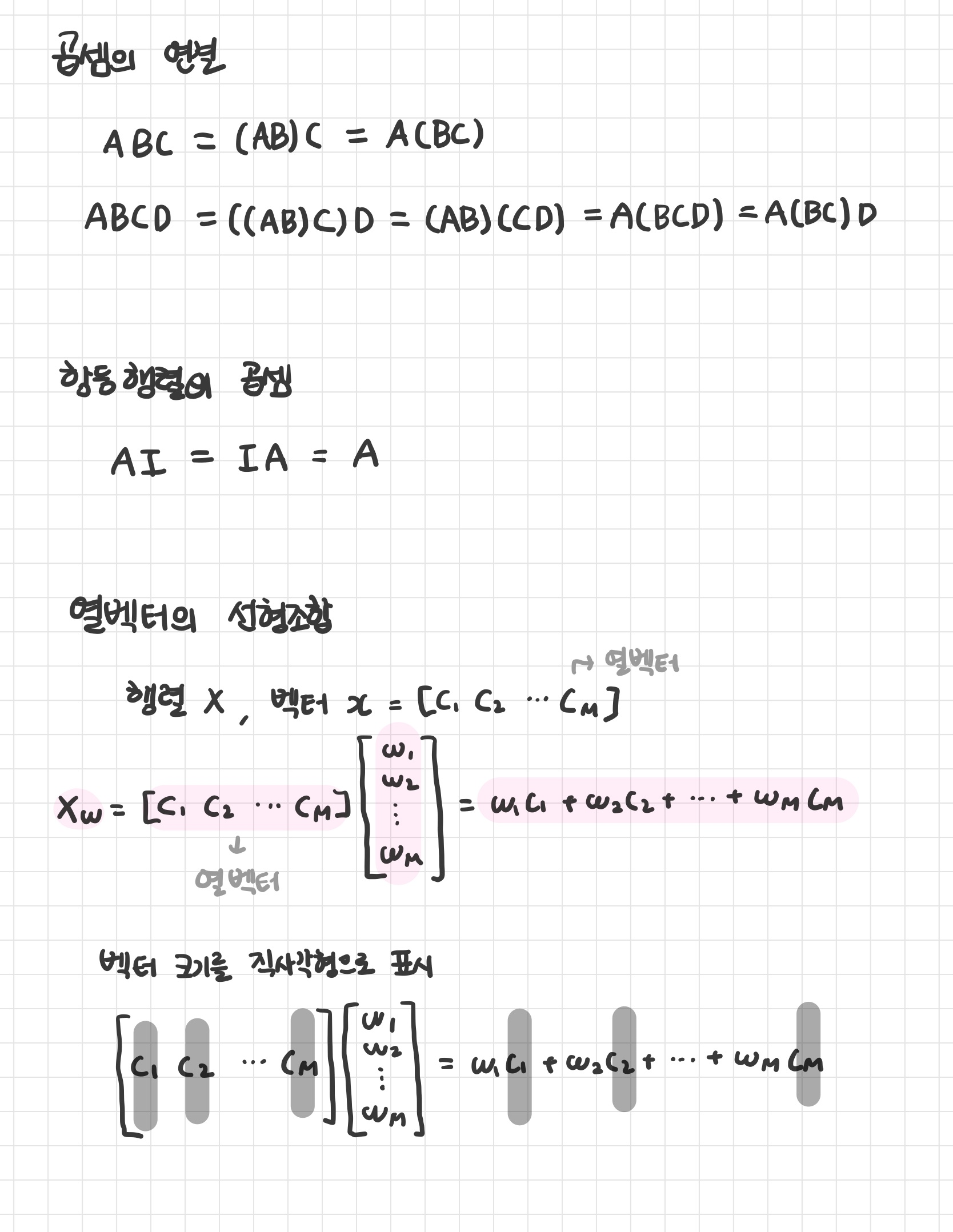
여러 개의 벡터에 대한 가중합 동시 계산

잔차

예측치와 실제값(target)의 차이를 오차 혹은 잔차

잔차 제곱

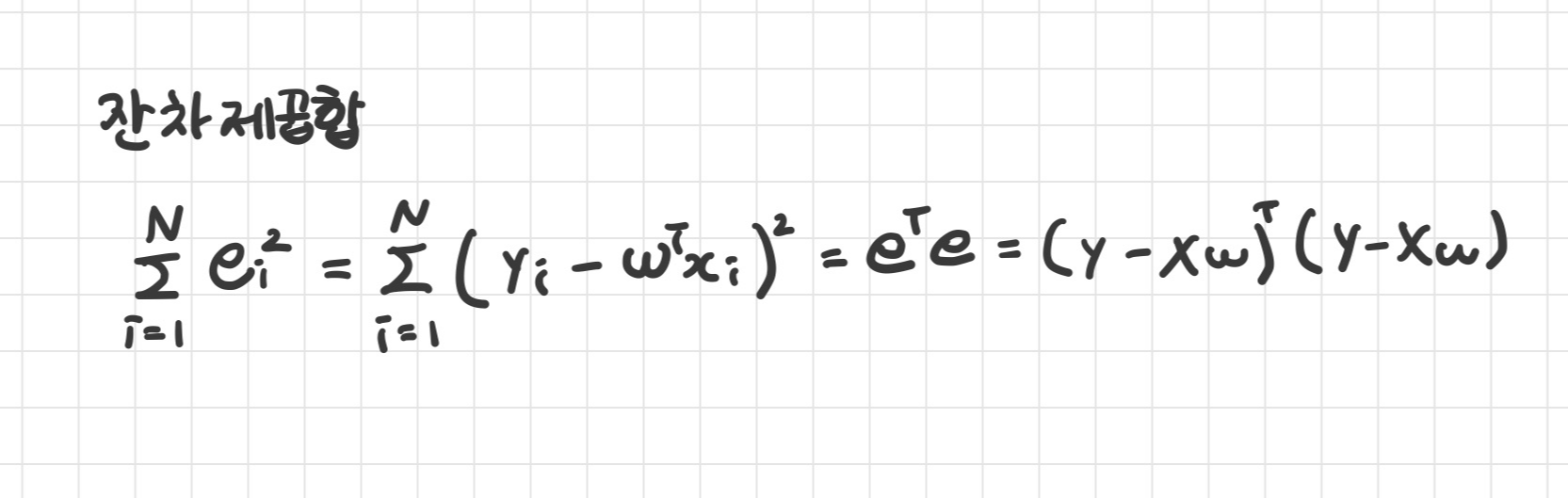
이차형식

어떤 벡터와 정방행렬이 '행벡터 x 정방행렬 x 열벡터' 형식으로 된 것

부분행렬

2.3 행렬의 성질

정부호와 준정부호

- 행렬은 여러 숫자로 이루어져 있으므로 실수처럼 부호나 크기를 정의하기 어렵

- 하지만 부호/크기와 유사한 개념은 정의할 수 있음

영 벡터가 아닌 모든 벡터 x에 대해 다음 부등식이 성립하면 행렬 A가 양의 정부호(positive definite)
(등호 포함시 양의 준정부호)
보통 대칭행렬에 대해서만 양의 정부호와 준정부호를 정의

- 행렬의 부호와 마찬가지로 행렬 크기를 정의하는 일도 어렵

- 놈, 대각합, 행렬식 연산이 행렬을 입력받아 크기와 유사한 개념의 숫자 계산

행렬 놈

행렬 A에 대해 다음 식으로 정의되는 숫자
행렬 놈에도 여러 정의가 있는데 여기에서는 요소별 행렬 놈(entrywise matrix norm) 정의 따름
p = 2인 놈 : 프로베니우스 놈

놈의 정의에서 알 수 있는 것

놈은 항상 0보다 같거나 크다
벡터의 놈의 제곱이 벡터의 제곱합과 같다
놈을 최소화하는 것은 벡터의 제곱합을 최소화하는 것과 같다

명령어 norm( )

놈의 정식 정의

놈의 값은 0 이상이다. 영행렬일 때만 놈의 값이 0이 된다.
행렬에 스칼라를 곱하면 놈의 값도 그 스칼라의 절댓값을 곱한 것과 같다.
행렬의 합의 놈은 각 행렬의 놈의 합보다 작거나 같다.
정방행렬의 곱의 놈은 각 정방행렬의 놈의 곱보다 작거나 같다.

대각합

대각합(trace)

정방행렬에 대해서만 정의
대각원소의 합으로 계산
ex) N차원 항등행렬의 대각합은 N
대각합을 구할 때는 절댓값을 취하거나 제곱을 하지 않기 때문에 대각합의 값은 놈과 달리 음수가 될 수도 있다.

대각합의 성질

스칼라를 곱하면 대각합은 스칼라와 원래 대각합의 곱이다.
전치연산을 해도 대각합이 달라지지 않는다.
두 행렬의 합의 대각합은 두 행렬의 대각합의 합이다.
두 행렬의 곱의 대각합은 행렬의 순서를 바꾸어도 달라지지 않는다.
세 행렬의 곱의 대각합은 다음과 같이 순서를 순환시켜도 달라지지 않는다.

특히 마지막 식은 트레이스 트릭(trace trick)

이차형식(quadrtic form)의 미분을 구하는 데 유용하게 사용됨
두 식에서는 A, B, C가 각각 정방행렬일 필요는 없음
최종적으로 대각합을 구하는 행렬만 정방행렬이면 됨

이차형식의 트레이스 트릭 공식

trace( ) 명령

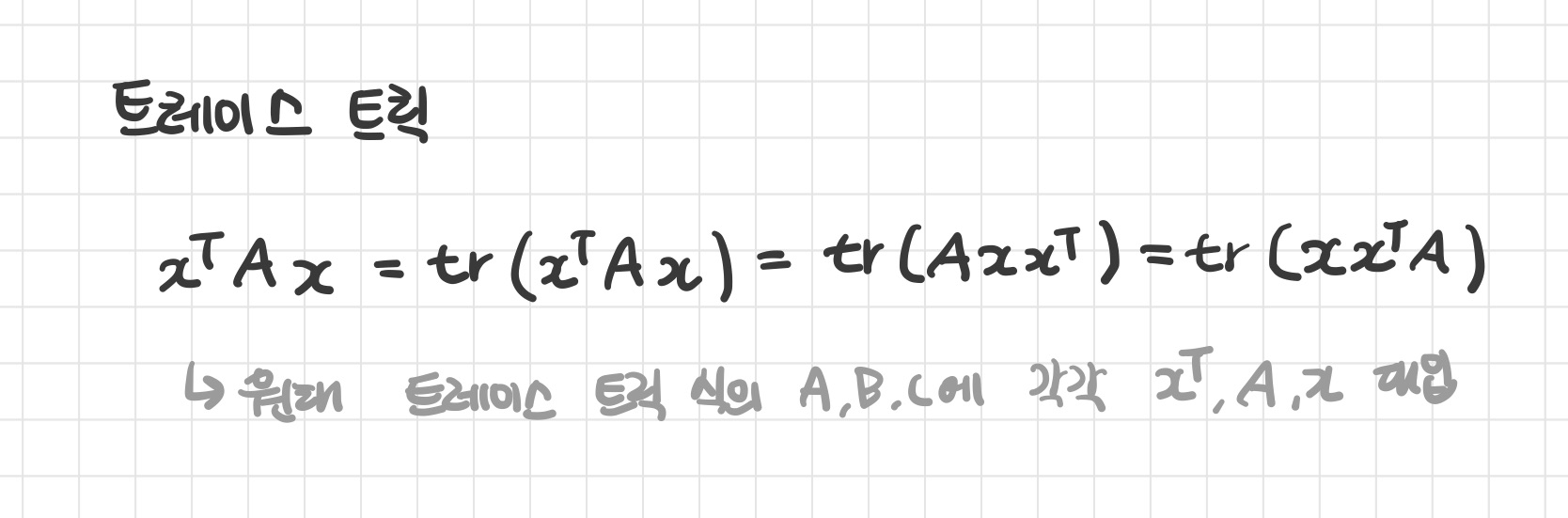
행렬식

행렬에서 임의의 행 하나를 선택하거나 임의의 열 하나를 선택한 다음 이 값에 가중치를 곱하여 더한 것
가중치로 사용된 M은 마이너(minor, 소행렬식)라고 하며 정방행렬 A에서 i행과 j열을 지워서 얻어진 (원래의 행렬보다 크기가 1만큼 작은) 행렬의 행렬식
마이너값도 행렬식이므로 마찬가지로 위의 정의를 이용해 계산
이처럼 점점 크기가 작은 행렬의 행렬식을 구하다 보면 스칼라인 행렬이 나오게 되는데, 행렬식의 값이 자기 자신이 됨
→ 행렬식을 구하는 방법은 재귀적(recursive)
여인수(그림)

행렬식의 값도 대각합과 마찬가지로 음수가 될 수 있다.

행렬식의 성질

전치행렬의 행렬식은 원래 행렬의 행렬식과 같다.
항등행렬의 행렬식은 1이다.
두 행렬의 곱의 행렬식은 각 행렬의 행렬식의 곱과 같다.
역행렬은 원래 행렬과 그림의 관계를 만족하는 정방행렬을 말한다. I는 항등행렬이다.
역행렬의 행렬식은 원래 행렬의 행렬식의 역수와 같다.

위 식은 역행렬의 정의와 여인수 전개식을 사용하여 증명할 수 있다.

2.4 선형 연립방정식과 역행렬

선형 예측 모형

입력 데이터 벡터와 가중치 벡터의 내적으로 계산된 예측값이 실제 출력 데이터와 유사한 값을 출력하도록 하는 모형

올바른 선형 예측 모형의 가중치 벡터 구하는 방법

연립방정식
역행렬

선형 연립방정식

복수의 미지수를 포함하는 복수의 선형 방정식

역행렬

항상 존재하는 것이 아님. 행렬 A에 따라서는 존재하지 않을 수도 있음.

가역행렬 (invertible matrix)

역행렬이 존재하지 않는 행렬
= 정칙행렬(regular matrix), 비특이 행렬(non-invertible matrix), 특이행렬(singular matrix), 퇴화행렬(degenerate matrix)

[연습문제]

대각행렬의 역행렬은 각 대각성분의 역수로 이루어진 대각행렬과 같다.

역행렬의 성질

(행렬 A, B, C는 모두 각각 역행렬이 존재한다고 가정)

전치행렬의 역행렬은 역행렬의 전치행렬과 같다. 따라서 대칭행렬의 역행렬도 대칭행렬이다.
두 개 이상의 정방행렬의 곱은 같은 크기의 정방행렬이 되는데 이러한 행렬의 곱의 역행렬은 다음 성질이 성립한다.

역행렬의 계산

증명은 생략
여인수로 이루어진 행렬 C를 여인수 행렬(matrix of cofactors, cofactor matrix, ccomatrix)
여인수 행렬의 전치행렬 C^T를 어드조인트행렬(adjoint matrix, adjugate matrix, 수반행렬), adj(A)로 표기
(A) = 0 이면 역수가 존재하지 않음
→ 역행렬은 행렬식이 0이 아닌 경우에만 존재한다.

역행렬에 대한 정리

셔먼-모리슨(Sherman-Morrison) 공식
우드베리(Woodbuty) 공식
분할행렬의 역행렬

넘파이를 사용한 역행렬 계산

inv( ) : 넘파이의 linalg 서브패키지의 역행렬 구하는 명령어

import numpy as np

A = np.array([[1, 1, 0], [0, 1, 1], [1, 1, 1]])
A
array([[1, 1, 0],
       [0, 1, 1],
       [1, 1, 1]])
       
Ainv = np.linalg.inv(A)
Ainv
array([[ 0., -1.,  1.],
       [ 1.,  1., -1.],
       [-1.,  0.,  1.]])

역행렬과 선형 연립방정식의 해

선형 연립방정식에서 미지수 수와 방정식 수가 같다면 계수행렬 A는 정방행렬
행렬 A의 역행렬이 존재한다면 역행렬 정의를 이용해 선형 연립방정식 해를 다음처럼 구할 수 있음
행렬과 벡터의 순서에 주의

넘파이를 이용해 앞의 선형 연립방정식의 해 x를 구하는 방법

벡터를 원래의 연립방정식에 대입하여 상수벡터 B와 값이 일치하는지 확인

import numpy as np

A = np.array([[1, 1, 0], [0, 1, 1], [1, 1, 1]])
A
array([[1, 1, 0],
       [0, 1, 1],
       [1, 1, 1]])
       
b = np.array([[2], [2], [3]])
b
array([[2],
       [2],
       [3]])
       
x = Ainv @ b
x
array([[1.],
       [1.],
       [1.]])
       
A @ x - b
array([[0.],
       [0.],
       [0.]])

lstsq( ) 명령어

입력 : 행렬 A와 B
출력
- 최소자승문제(least square problem)의 답 x
- 잔차 제곱합(residual sum of sdquares) resid
- 랭크 rank
- 특잇값(singular value) s
미지수와 방정식 개수 동일 & 행렬 A의 역행렬이 존재
→ 최소자승문제의 답과 선형 연립방정식 답 같으므로 lstsq( ) 명령으로 선형 연립방정식 풀 수도 있음
(뒤에서 자세히 설명할 내용)

lstsq( ) 명령으로 구한 답이 inv( ) 명령으로 구한 답과 같음

lstsq( ) 명령을 사용하는 것이 inv( ) 명령을 사용하는 것보다 수치오차 적고 코드 간단
선형 연립방정식 해를 구할 때도 lstsq( ) 명령 사용하는 것 권장

x, resid, rank, s = np.linalg.lstsq(A, b)
x
array([[1.],
       [1.],
       [1.]])

선형 연립방정식과 선형 예측 모형

선형 예측 모형의 가중치벡터를 구하는 문제는 선형 연립방정식을 푸는 것과 같다

ex) 입력차원이 N인 특징벡터 N개를 입력 데이터, 입력에 대응하는 목푯값벡터를 출력하는 선형 예측 모형
- 이 예측 모형의 가중치벡터 w를 찾는 것은 계수행렬이 X, 미지수벡터가 w, 상수벡터가 y인 선형 연립방정식 답을 찾는 것과 같다.
- 만약 계수행렬, 여기서는 특징행렬 X의 역행렬이 존재한다면 가중치벡터를 구할 수 있다.

미지수 수와 방정식 수

지금까지는 '미지수 수=방정식 수' 선형 연립방정식에 대해서만 생각

만약 다르다면 어떻게 해야 할까?

연립방정식 세 종류(미지수 수와 방정식 수를 고려)

방정식 수가 미지수 수와 같다. (N = M)
방정식 수가 미지수 수보다 적다. (N < M)
방정식 수가 미지수 수보다 많다. (N > M)

1. 방정식 수가 미지수 수와 같다. (N = M)

앞에서 다룬 경우

2. 방정식 수가 미지수 수보다 적다. (N < M)

무수히 많은 해가 존재할 수 있음

ex)

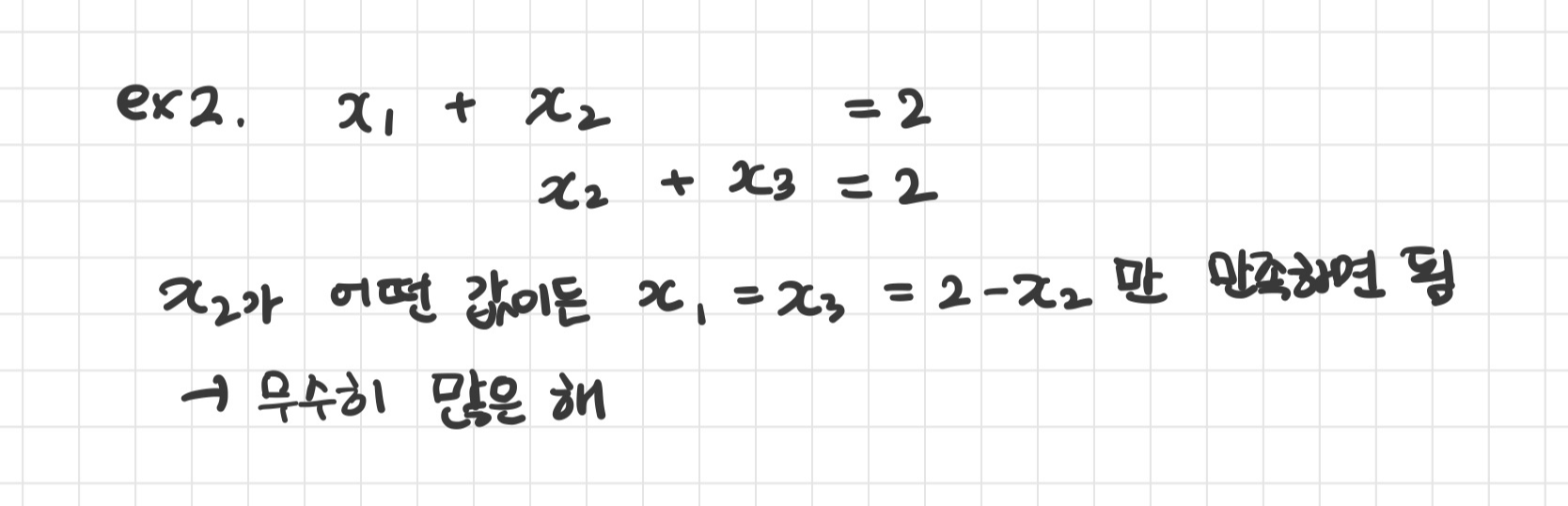
3. 방정식 수가 미지수 수보다 많다. (N > M)

2번과 반대로 모든 조건을 만족하는 해가 하나도 없을 수도 있음

ex)

선형 예측 모형을 구하는 문제
= 계수행렬이 특징행렬 X, 미지수벡터가 가중치벡터인 w인 선형 연립방정식 문제

But, 데이터 수는 입력차원보다 큰 경우가 많음
ex) 면적, 층수, 한강이 보이는지 여부로 집값 결정하는 모형
- 3가구의 아파트 가격만 조사하는 경우 없음
- 보통 10 ~ 100 가구 아파트 격을 수집하여 이용
선형 예측 모형을 구할 때 3번과 같은 경우 많음
이때는 선형 연립방정식 해가 존재하지 않으므로, 선형 연립방정식을 푸는 방식으로는 선형 예측 모형의 가중치벡터를 구할 수 없음

최소자승문제

선형 연립방정식의 해가 존재하지 않는다면 선형 예측 모형은 어떻게 구할까?

→ 차이를 최소화하는 문제로 바꾸어 해결

'미지수 수 < 방정식 수' 라서 선형 연립방정식으로 풀 수 없는 문제

→ 좌변과 우변의 차이를 최소화하는 문제로 바꾸어 풀이

잔차 : 예측값과 목푯값의 차이
잔차는 벡터, 최소자승문제에서는 벡터의 크기 중에서 벡터의 놈을 최소화하는 문제를 출이
놈 최소화 = 놈**2 최소화 → 여기에서는 잔차제곱합이 놈의 제곱

넘파이의 lstsq( ) 명령은 이러한 최소자승문제를 푸는 명령어

A = np.array([[1, 1, 0], [0, 1, 1], [1, 1, 1], [1, 1, 2]])
A
array([[1, 1, 0],
       [0, 1, 1],
       [1, 1, 1],
       [1, 1, 2]])
       
       
b = np.array([[2], [2], [3], [4.1]])
b
array([[2. ],
       [2. ],
       [3. ],
       [4.1]])
       
# 의사역행렬을 직접 계산하여 해를 구함
Apinv = np.linalg.inv(A.T @ A) @ A.T
Apinv
array([[ 0.33333333, -1.        ,  0.33333333,  0.33333333],
       [ 0.5       ,  1.        ,  0.        , -0.5       ],
       [-0.5       ,  0.        ,  0.        ,  0.5       ]])
       
x = Apinv @ b
x
array([[1.03333333],
       [0.95      ],
       [1.05      ]])

# 이 해를 이용하여 b값을 구하면 다음처럼 우변과 소수점 아래 한자리 오차 내에 있는 것 확인
A @ x
array([[1.98333333],
       [2.        ],
       [3.03333333],
       [4.08333333]])

# lstsq() 명령으로 바로 구해도 같은 값
x, resid, rank, s = np.linalg.lstsq(A, b)
x
array([[1.03333333],
       [0.95      ],
       [1.05      ]])

# 위 코드에서 resid는 잔차벡터의 e = Ax - b의 제곱합, 즉 놈의 제곱
resid, np.linalg.norm(A @ x - b) ** 2
(array([0.00166667]), 0.001666666666666655)