[AI 기초] 7. 합성곱 신경망(CNN)

AI/AI 기초

[AI 기초] 7. 합성곱 신경망(CNN)

kk_______yy 2024. 1. 30. 12:28

7.1 전체 구조

완전 연결(fully-connected, 전결합) : 인접하는 계층의 모든 뉴런과 결합

[그림 7-1] 완전연결 계층(Affine 계층)으로 이뤄진 네트워크의 예

완전연결 신경망

Affine 계층 뒤에 활성화 함수를 갖는 ReLU 계층 (혹은 Sigmoid 계층)이 이어짐
이 그림 Affine-ReLU 조합 4개, 마지막 5번째 층은 Affine 계층에 이어 소프트맥스 계층에서 최종 결과(확률) 출력

[그림 7-2] CNN으로 이뤄진 네트워크의 예 : 합성곱 계층과 풀링 계층이 새로 추가(회색)

CNN : 합성곱 계층(Conv)과 풀링 계층(Pooling)이 추가됨

Conv - ReLU - (Pooling) 흐름으로 연결(풀링 계층은 생략하기도 함)
Affine - ReLU 연결이 Conv - ReLU - (Pooling)으로 바뀜
출력에 가까운 층에서는 지금까지의 'Affine - ReLU' 구성을 사용할 수 있음

7.2 합성곱 계층

7.2.1 완전연결 계층의 문제점

'데이터의 형상이 무시'된다는 사실

ex) 이미지

세로 * 가로 * 채널(색상)의 3차원 데이터
3차원 형상에는 공간적 정보 담김(공간적으로 가까운 픽셀은 값이 비슷, RGB 각 채널은 서로 밀접하게 관련, ...)
완전연결 계층 : 입력 시 3차원 데이터를 평평한 2차원 데이터로 평탄화해줘야 함
→ 형상을 무시하고 모든 입력 데이터를 동등한 뉴련(같은 차원의 뉴런)으로 취급하여 형상에 담긴 정보 살릴 수 없음
합성곱 계층 : 형상 유지, 이미지 3차원 데이터로 입력받아 다음 계층에도 3차원 데이터로 전달

CNN

특징 맵(feature map) : 합성곱 계층의 입출력 데이터
입력 특징 맵(input feature map) : 합성곱 계층의 입력 데이터
출력 특징 맵(output feature map) : 출력 데이터

7.2.2 합성곱 연산

필터 = 커널
합성곱 연산은 필터의 윈도우(window)를 일정 간격으로 이동해가며 입력 데이터에 적용
입력과 필터에서 대응하는 원소끼리 곱한 후 그 총합 구함(단일 곱셈-누산, fused multipy-add, FMA)
그 결과를 출력의 해당 장소에 저장

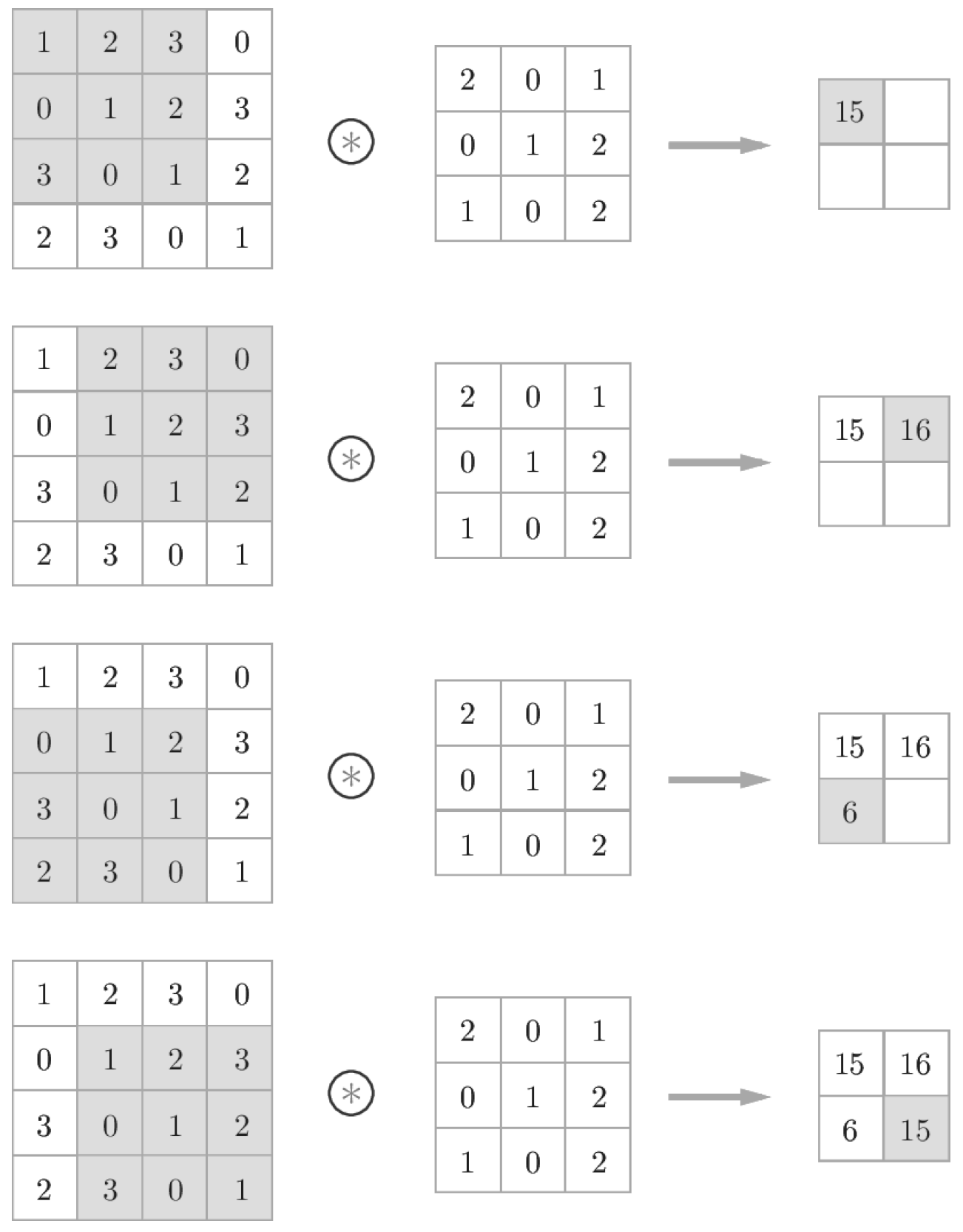
CNN에서는 필터의 매개변수가 그동안의 '가중치'에 해당(편향 x인 그림)

[그림 7-5] 합성곱 연산의 편향 : 필터를 적용한 원소에 고정값(편향)을 더한다

편향은 필터를 적용한 후의 데이터에 더해짐
편향은 항상 하나(1x1)만 존자
하나의 값을 필터를 적용한 모든 원소에 더함

7.2.3 패딩

패딩(padding) : 합성곱 연산을 수행하기 전에 입력 데이터 주변을 특정 값(예컨대 0)으로 채우는 것

ex) 폭 1짜리 패딩 : 입력 데이터 사방 1픽셀을 특정 값으로 채우는 것

[그림 7-6] 합성곱 연산의 패딩 처리 : 입력 데이터 주위에 0을 채운다(패딩은 점선 표시, 그 안의 값 0은 생략)

(4, 4) 크기의 입력 데이터에 폭이 1인 패딩을 적용 → (3, 3) 크기의 필터 → (4, 4) 크기의 출력 데이터 생성

cf)

패딩 2 → 입력 데이터 크기 (8, 8)

패딩 3 → 입력 데이터 크기 (10, 10)

* NOTE

패딩은 주로 출력 크기 조정 목적으로 사용
합성곱 연산을 몇 번이나 되풀이하면 입력 데이터가 줄어드는 문제
이를 막기 위해 패딩 사용
= 입력 데이터의 공간적 크기를 고정한 채로 다음 계층에 전달

7.2.4 스트라이드

스트라이드(stride, 보폭) : 필터를 적용하는 위치의 간격

ex) 스트라이드 2 : 필터를 적용하는 윈도우가 두 칸씩 이동

(7, 7) 크기의 입력 데이터 → 스트라이드 2로 설정한 필터 → (3, 3) 크기의 출력 데이터 생성

스트라이트를 키우면 출력 크기는 작아짐
패딩을 크게 하면 출력 크기 커짐

이를 수식화해보자

입력 크기 (H, W)
필터 크기(FH, FW)
출력 크기 (OH, OW)
패딩 P
스트라이드 S

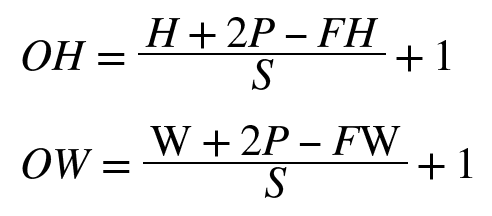
ex)

입력 : (4, 4)
패딩 : 1
스트라이드 : 1
필터 : (3, 3)

OH = ((4+ 2*1 -3) / 1) + 1 = 4

OW = ((4+ 2*1 -3) / 1) + 1 = 4

* 주의

정수로 나눠떨어지는 값이어야 하지만, 반올림 등의 구현기법도 존재

7.2.5 3차원 데이터의 합성곱 연산

3차원 데이터를 다루는 합성곱 연산을 살펴보자

채널 쪽으로 특징 맵이 여러 개 있다면 입력 데이터와 필터의 합성곱 연산을 채널마다 수행, 그 결과를 더해서 하나의 출력

* 주의

입력 데이터의 채널 수와 필터의 채널 수가 같아야 함
필터 자체의 크기는 원하는 값으로 설정할 수 있음(단, 모든 채널의 크기 동일해야 함)

7.2.6 블록으로 생각하기

3차원 합성곱 연산은 데이터와 필터를 직육면체 블록이라고 생각하면 쉬움
3차원 데이터를 다차원 배열로 나타낼 때는 (채널, 높이, 너비) 순서로 작성

ex)

데이터의 형상 (C, H, W)
필터의 형상 (C, FH, FW)

[그림 7-10] 합성곱 연산을 직육면체 블록으로 생각한다. 블록의 형상에 주의할 것!

이 예에서 출력 데이터는 한 장의 특징 맵(=채널이 1개인 특징 맵)

그렇다면, 합성곱 연산의 출력으로 다수의 채널을 내보내려면 어떻게 해야 할까?

필터(가중치)를 다수 사용하는 것

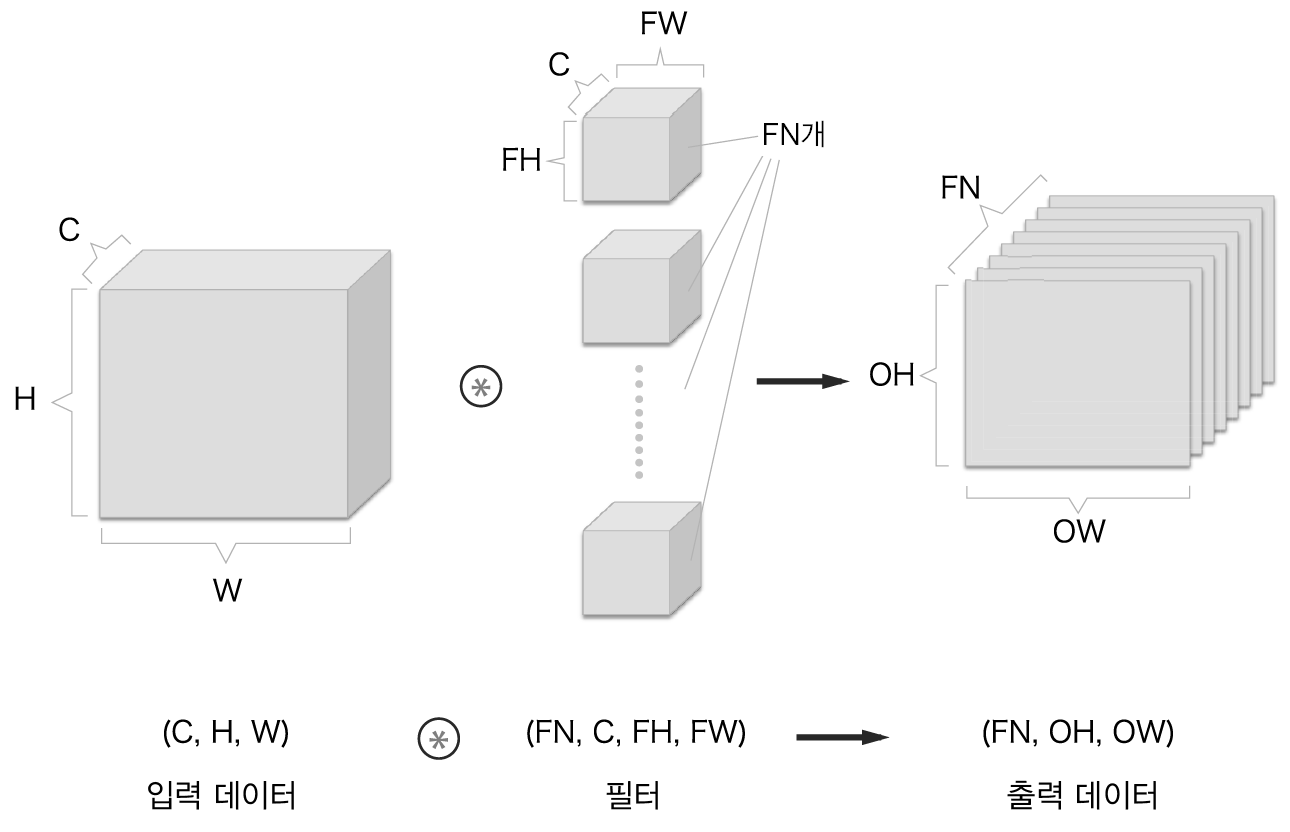
필터를 FN개 적용하면 출력 맵도 FN개 생성

FN개의 맵을 모으면 형상이 (FN, OH, OW)인 블록 완성
이 완성된 블록을 다음 계층으로 넘기겠다는 것이 CNN의 처리 흐름

합성곱 연산에서는 필터의 수도 고려해야 함

필터의 가중치 데이터는 4차원 데이터 (출력 채널 수, 입력 채널 수, 높이, 너비) 순서

ex) 채널 수 3, 크기 5x5, 필터 20개 있다면 (20, 3, 5, 5)로 작성

합성곱 연산에도 (완전연결 계층과 마찬가지로) 편향 쓰임

편향은 채널 하나에 값 하나씩으로 구성
이 예에서는 편향의 형상 (FN, 1, 1), 필터의 출력 결과의 형상 (FN, OH, OW)
이 두 블록을 더하면 편향의 각 값이 필터의 출력인 (FN, OH, OW) 블록의 대응 채널의 원소 모두에 더해짐

cf)

형상이 다른 블록의 덧셈은 넘파이의 브로드캐스트 기능으로 쉽게 구현

7.2.7 배치 처리

합성곱 연산도 배치 처리를 지원해보자.

신경망 처리에서는 입력 데이터를 한 덩어리로 묶어 배치로 처리
이를 통해 처리 효율을 높이고, 미니배치 방식의 학습도 지원
각 계층을 흐르는 데이터의 차원을 하나 늘려 4차원 데이터로 저장
→ (데이터 수, 채널 수, 높이, 너비) 순으로 저장

데이터가 N개일 때 [그림 7-12]를 배치 처리하면 데이터가 [그림 7-13] 형태로

각 데이터의 선두에 배치용 차원을 추가
이처럼 데이터는 4차원 데이터가 하나 흐를 때마다 데이터 N개에 대한 합성곱 연산이 이루어짐
즉, N회 분의 처리를 한 번에 수행

7.3 풀링 계층

풀링 : 세로, 가로 방향의 공간을 줄이는 연산

ex) [그림 7-14]와 같이 2x2 영역을 원소 하나로 집약하여 공간의 크기 줄임

위는 2x2 최대 풀링(max pooling)을 스트라이드 2로 처리하는 순서

최대 풀링은 최댓값(max)을 구하는 연산으로, 2x2는 대상 영역의 크기를 의미
스트라이드는 2로 설정, 2x2 윈도우가 원소 2칸 간격으로 이동

cf) 풀링의 윈도우 크기와 스트라이드는 같은 값으로 설정하는 것이 보통

ex) 윈도우 3x3이면 스트라이드 3, 윈도우 4x4이면 스트라이드 4

학습해야 할 매개변수가 없다

풀링 계층은 합성곱 계층과 달리 학습해야 할 매개 변수가 없음
대상 영역에서 최댓값이나 평균을 취하는 명확한 처리

채널 수가 변하지 않는다

풀링 연산은 입력 데이터의 채널 수 그대로 출력 데이터로 내보냄
아래 그림처럼 채널마다 독립적으로 계산

입력 변화에 영향을 적게 받는다(강건하다)

입력 데이터가 조금 변해도 풀링의 결과는 잘 변하지 않음
다음 그림은 입력 데이터의 차이(데이터가 오른쪽으로 1칸씩 이동)를 풀링이 흡수해 사라지게 하는 모습

[그림 7-16] 입력 데이터가 가로롤 1원소만큼 어긋나도 출력은 같다(데이터에 따라서는 다를 수도 있다).

7.4 합성곱/풀링 계층 구현하기

합성곱 계층과 풀링 계층을 '트릭'을 사용해 쉽게 구현해보자

7.4.1 4차원 배열

CNN에서 계층 사이를 흐르는 데이터는 4차원

ex) (10, 1, 28, 28) : 높이 28, 너비 28, 채널 1개, 이러한 데이터 10개

x = np.random.rand(10, 1, 28, 28)    # 무작위로 데이터 생성
x.shape
>>> (10, 1, 28, 28)

# 첫 번째 데이터 접근
x[0].shape    # (1, 28, 28)
# 두 번째 데이터 접슨
x[1].shape    # (1, 28, 28)

#첫 번째 데이터의 첫 채널의 공간 데이터에 접근
x[0, 0]       # 또는 x[0][0]

7.4.2 im2col로 데이터 전개하기

for문을 겹겹히 써서 합성곱 연산이 곧이곧대로 구현하기는 귀찮고, 성능이 떨어짐
im2col 이라는 편의 함수를 사용해 간단하게 구현

im2col

입력 데이터를 필터링(가중치 계산)하기 좋게 전개하는(펼치는) 함수
아래 그림과 같이 3차원 입력 데이터에 im2col을 적용하면 2차원 행렬로 바뀜

im2col은 필터링하기 좋게 입력 데이터를 전개
= 입력 데이터에서 필터를 적용하는 영역(3차원 블록)을 한 줄로 늘어놓음([그림 7-18])
이 전개를 필터 적용 모든 영역에서 수행하는 것이 im2col

[그림 7-18]에서는 스트라이드를 크게 잡아 필터의 적용 영역이 겹치지 않게 함
실제 상황에서는 영역이 겹치는 경우가 대부분
→ im2col로 전개한 후 원소 수가 원래 블록의 원소 수보다 많아짐

장단점

장점 : 컴퓨터는 큰 행렬을 묶어서 계산하는 데 탁월, 선형 대수 라이브러리를 활용해 효율 높일 수 있음
단점 : 메모리를 더 많이 소비

* NOTE

im2col = 'image to column'

[그림 7-19] 합성곱 연산의 필터 처리 상세 과정 : 필터를 세로로 1열로 전개하고, im2col이 전개한 데이터와 행렬 곱을 계산합니다. 마지막으로 출력 데이터를 변형(reshape)합니다.

합성곱 계층의 구현 흐름

im2col로 입력 데이터를 전개
합성곱 계층의 필터(가중치)를 1열로 전개
두 행렬 곱을 계산
= 완전연결 계층의 Affine 계층에서와 거의 동일
im2col 방식으로 출력한 결과는 2차원 행렬
CNN은 데이터를 4차원 배열로 저장하므로, 2차원인 출력 데이터를 4차원으로 변형(reshape)

7.4.3 합성곱 계층 구현하기

im2col 함수의 인터페이스

: 필터 크기, 스트라이드, 패딩을 고려하여 입력 데이터를 2차원 배열로 전개

def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
    """다수의 이미지를 입력받아 2차원 배열로 변환한다(평탄화).
    
    Parameters
    ----------
    input_data : 4차원 배열 형태의 입력 데이터(이미지 수, 채널 수, 높이, 너비)
    filter_h : 필터의 높이
    filter_w : 필터의 너비
    stride : 스트라이드
    pad : 패딩
    
    Returns
    -------
    col : 2차원 배열
    """
    N, C, H, W = input_data.shape
    out_h = (H + 2*pad - filter_h)//stride + 1
    out_w = (W + 2*pad - filter_w)//stride + 1

    img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
    col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))

    for y in range(filter_h):
        y_max = y + stride*out_h
        for x in range(filter_w):
            x_max = x + stride*out_w
            col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]

    col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
    return col

im2col을 실제로 사용해보자

첫 번째 데이터 : 배치 크기 1(데이터 1개), 채널 3개, 높이-너비 7x7
두 번째 데이터 : 배치 크기 10, 나머지 동일

→ 두 경우 모두 2번째 차원의 원소 75개 = 필터의 원소 수(채널 3개, 5x5 데이터)

→ 배치 크기가 1일 때는 im2col의 결과의 크기가 (9, 75)이고, 10일 때는 그 10배인 (90, 75) 크기의 데이터 저장

import xyx, os
sys.path.append(os.pardir)
from common.utio import im2col

x1 = np.random.rand(1, 3, 7, 7)    # (데이터 수, 채널 수, 높이, 너비)
col1 = im2col(x1, 5, 5, stride=1, pad=0)
print(col1.shape)    # (9, 75)

x2 = np.random.rand(10, 3, 7, 7)    # 데이터 10개
col2 = im2col(x2, 5, 5, stride=1, pad=0)
print(col2.shape)    # (90, 75)

im2col을 사용한 합성곱 계층 구현

합성곱 계층은 필터(가중치), 편향, 스트라이드, 패딩을 인수로 받아 초기화
필터는 (FN, C, FH, FW)의 4차원 형상 : (FN 필터 개수, C 채널, FH 필터 높이, FW필터 너비)
필터 전개하는 부분(#중요#)은 각 필터 블록을 1줄로 펼쳐 세움
reshape의 두 번째 인수를 -1로 지정
- -1 지정하면, 다차원 배열의 원소 수가 변환 후에도 똑같이 유지되도록 적절히 묶어줌
- (10, 3, 5, 5) 형상의 다차원 배열 W의 원소 수는 총 750개, reshape(10, -1)을 호출하면 750개 원소를 10묶음으로
- 즉, 형상이 (10, 75)인 배열로 만들어줌

class convolution:
    def __init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad
        
    def forward(self, x):
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        out_h = int(1 + (H + 2*self.pad - FH) / self.stride)
        out_w = int(1 + (W + 2*self.pad - FW) / self.stride)
        
        #################중요#################
        col = im2col(x, FH, FW, self.stride, self.pad)
        col_W = self.W.reshape(FN, -1).T    # 필터 전개
        out = np.dot(col, col_W) + self.b
        #################중요#################
        
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
        
        return out

forward 구현의 마지막에서는 출력 데이터를 적절한 형상으로 바꿔줌
- 넘파이 transpose 함수 사용 : 다차원 배열의 축 순서 바꿔주는 함수
- 인덱스를 지정하여 축의 순서를 변경

[그림 7-20] 넘파이의 transpose 함수로 축 순서 변경하기 : 인덱스(번호)로 축의 순서를 변경한다.

합성곱 계통의 역전파 구현은 Affine 계층의 구현과 공통점 많음(아래 코드 참고)

* 주의

합성곱 계층의 역전파에서는 im2col을 역으로 처리

class Convolution:
    def __init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad
        
        # 중간 데이터（backward 시 사용）
        self.x = None   
        self.col = None
        self.col_W = None
        
        # 가중치와 편향 매개변수의 기울기
        self.dW = None
        self.db = None

    def forward(self, x):
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        out_h = 1 + int((H + 2*self.pad - FH) / self.stride)
        out_w = 1 + int((W + 2*self.pad - FW) / self.stride)

        col = im2col(x, FH, FW, self.stride, self.pad)
        col_W = self.W.reshape(FN, -1).T

        out = np.dot(col, col_W) + self.b
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

        self.x = x
        self.col = col
        self.col_W = col_W

        return out

    def backward(self, dout):
        FN, C, FH, FW = self.W.shape
        dout = dout.transpose(0,2,3,1).reshape(-1, FN)

        self.db = np.sum(dout, axis=0)
        self.dW = np.dot(self.col.T, dout)
        self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)

        dcol = np.dot(dout, self.col_W.T)
        dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)

        return dx

7.4.4 풀링 계층 구현하기

풀링 계층 vs 합성곱 계층

공통점 : im2col을 사용해 입력 데이터 전개
차이점 : 풀링은 채널 쪽이 독립적, 풀링 적용 영역을 채널마다 독립적으로 전개

[그림 7-21] 입력 데이터에 풀링 적용 영역을 전개 (2x2 풀링의 예)

이렇게 전개한 후, 전개한 행렬에서 행별 최댓값을 구하고 적절한 형상으로 성형

풀링 계층 구현

입력 데이터를 전개
행별 최댓값을 구함
적절한 모양으로 성형

class Pooling:
    def __init__(self, pool_h, pool_w, stride=1, pad=0):
        self.pool_h = pool_h
        self.pool_w = pool_w
        self.stride = stride
        self.pad = pad
        
        self.x = None
        self.arg_max = None

    def forward(self, x):
        N, C, H, W = x.shape
        out_h = int(1 + (H - self.pool_h) / self.stride)
        out_w = int(1 + (W - self.pool_w) / self.stride)
        
        # 전개 (1)
        col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
        col = col.reshape(-1, self.pool_h*self.pool_w)
        
        arg_max = np.argmax(col, axis=1)
        
        # 최댓값 (2)
        out = np.max(col, axis=1)
        
        # 성형 (3)
        out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
    
        self.x = x
        self.arg_max = arg_max

        return out
        
    def backward(self, dout):
        dout = dout.transpose(0, 2, 3, 1)
        
        pool_size = self.pool_h * self.pool_w
        dmax = np.zeros((dout.size, pool_size))
        dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
        dmax = dmax.reshape(dout.shape + (pool_size,)) 
        
        dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
        dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
        
        return dx

* NOTE

최댓값 계산 : 넘파이 np.max 메서드
인수로 축(axis)을 지정할 수 있는데, 이 인수로 지정한 축마다 최댓값을 구할 수 있음
np.max(x, axis=1)과 같이 쓰면 입력 x의 1번째 차원의 축마다 최댓값 구함

backward 처리는 설명 생략

7.5 CNN 구현하기

합성곱 계층과 풀링 게층을 구현했으니, 이 계층들을 조합하여 손글씨 숫자를 인식하는 CNN을 조립해보자.

다음과 같은 구조의 CNN을 구현

* 합성곱 계층의 하이퍼파라미터는 딕셔너리 형태로 주어짐(conv_param)
즉, {'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1} 처럼 저장

초기화

초기화 인수로 주어진 합성곱 계층의 하이퍼파라미터를 딕셔너리에서 꺼냄
합성곱 계층의 출력 크기 계산
가중치 매개변수를 초기화
- 학습에 필요한 매개변수는 1번째 층의 합성곱 계층 & 나머지 두 완전연결 계층의 가중치와 편향
각각 층의 가중치와 편향을 W, b로 저장
CNN을 구성하는 계층들을 생성

class SimpleConvNet:
    """단순한 합성곱 신경망
    
    conv - relu - pool - affine - relu - affine - softmax
    
    Parameters
    ----------
    input_size : 입력 크기（MNIST의 경우엔 784）
    hidden_size_list : 각 은닉층의 뉴런 수를 담은 리스트（e.g. [100, 100, 100]）
    output_size : 출력 크기（MNIST의 경우엔 10）
    activation : 활성화 함수 - 'relu' 혹은 'sigmoid'
    weight_init_std : 가중치의 표준편차 지정（e.g. 0.01）
        'relu'나 'he'로 지정하면 'He 초깃값'으로 설정
        'sigmoid'나 'xavier'로 지정하면 'Xavier 초깃값'으로 설정
    """
    def __init__(self, input_dim=(1, 28, 28), 
                 conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
                 hidden_size=100, output_size=10, weight_init_std=0.01):
        filter_num = conv_param['filter_num']
        filter_size = conv_param['filter_size']
        filter_pad = conv_param['pad']
        filter_stride = conv_param['stride']
        input_size = input_dim[1]
        conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
        pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))

        # 가중치 초기화
        self.params = {}
        self.params['W1'] = weight_init_std * \
                            np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
        self.params['b1'] = np.zeros(filter_num)
        self.params['W2'] = weight_init_std * \
                            np.random.randn(pool_output_size, hidden_size)
        self.params['b2'] = np.zeros(hidden_size)
        self.params['W3'] = weight_init_std * \
                            np.random.randn(hidden_size, output_size)
        self.params['b3'] = np.zeros(output_size)

        # 계층 생성
        self.layers = OrderedDict()
        self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
                                           conv_param['stride'], conv_param['pad'])
        self.layers['Relu1'] = Relu()
        self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
        self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
        self.layers['Relu2'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])

        self.last_layer = SoftmaxWithLoss()

추론을 수행하는 predict 메서드 & 손실 함수의 값을 구하는 loss 메서드 구현

x는 입력 데이터, t는 정답 레이블

predict 메서드
초기화 때 layers에 추가한 계층을 맨 앞에서부터 차레로 forward 메서드 호출
그 결과 다음 계층에 전달
loss 메서드
predict 메서드의 결과를 인수로 마지막 층의 forward 메서드 호출
첫 계층부터 마지막 계층까지 forward를 처리

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)

        return x

    def loss(self, x, t):
        """손실 함수를 구한다.

        Parameters
        ----------
        x : 입력 데이터
        t : 정답 레이블
        """
        y = self.predict(x)
        return self.last_layer.forward(y, t)

오차역전파법으로 기울기 구하는 구현

순전파와 역전파 반복
이전에 작성한 내용을, 순서대로 적절히 호출
마지막으로 grads라는 딕셔너리 변수에 각 가중치 매개변수의 기울기 저장

    def gradient(self, x, t):
        """기울기를 구한다(오차역전파법).

        Parameters
        ----------
        x : 입력 데이터
        t : 정답 레이블

        Returns
        -------
        각 층의 기울기를 담은 사전(dictionary) 변수
            grads['W1']、grads['W2']、... 각 층의 가중치
            grads['b1']、grads['b2']、... 각 층의 편향
        """
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.last_layer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 결과 저장
        grads = {}
        grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
        grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

        return grads

전체 코드 : SimpleConvNet으로 MNIST 데이터셋 학습

훈련 데이터에 대한 정확도 99.82%
시험 데이터에 대한 정확도 98.96%
작은 네트워크 치고 높은 성능

class SimpleConvNet:
    """단순한 합성곱 신경망
    
    conv - relu - pool - affine - relu - affine - softmax
    
    Parameters
    ----------
    input_size : 입력 크기（MNIST의 경우엔 784）
    hidden_size_list : 각 은닉층의 뉴런 수를 담은 리스트（e.g. [100, 100, 100]）
    output_size : 출력 크기（MNIST의 경우엔 10）
    activation : 활성화 함수 - 'relu' 혹은 'sigmoid'
    weight_init_std : 가중치의 표준편차 지정（e.g. 0.01）
        'relu'나 'he'로 지정하면 'He 초깃값'으로 설정
        'sigmoid'나 'xavier'로 지정하면 'Xavier 초깃값'으로 설정
    """
    def __init__(self, input_dim=(1, 28, 28), 
                 conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
                 hidden_size=100, output_size=10, weight_init_std=0.01):
        filter_num = conv_param['filter_num']
        filter_size = conv_param['filter_size']
        filter_pad = conv_param['pad']
        filter_stride = conv_param['stride']
        input_size = input_dim[1]
        conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
        pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))

        # 가중치 초기화
        self.params = {}
        self.params['W1'] = weight_init_std * \
                            np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
        self.params['b1'] = np.zeros(filter_num)
        self.params['W2'] = weight_init_std * \
                            np.random.randn(pool_output_size, hidden_size)
        self.params['b2'] = np.zeros(hidden_size)
        self.params['W3'] = weight_init_std * \
                            np.random.randn(hidden_size, output_size)
        self.params['b3'] = np.zeros(output_size)

        # 계층 생성
        self.layers = OrderedDict()
        self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
                                           conv_param['stride'], conv_param['pad'])
        self.layers['Relu1'] = Relu()
        self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
        self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
        self.layers['Relu2'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])

        self.last_layer = SoftmaxWithLoss()

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)

        return x

    def loss(self, x, t):
        """손실 함수를 구한다.

        Parameters
        ----------
        x : 입력 데이터
        t : 정답 레이블
        """
        y = self.predict(x)
        return self.last_layer.forward(y, t)

    def accuracy(self, x, t, batch_size=100):
        if t.ndim != 1 : t = np.argmax(t, axis=1)
        
        acc = 0.0
        
        for i in range(int(x.shape[0] / batch_size)):
            tx = x[i*batch_size:(i+1)*batch_size]
            tt = t[i*batch_size:(i+1)*batch_size]
            y = self.predict(tx)
            y = np.argmax(y, axis=1)
            acc += np.sum(y == tt) 
        
        return acc / x.shape[0]

    def numerical_gradient(self, x, t):
        """기울기를 구한다（수치미분）.

        Parameters
        ----------
        x : 입력 데이터
        t : 정답 레이블

        Returns
        -------
        각 층의 기울기를 담은 사전(dictionary) 변수
            grads['W1']、grads['W2']、... 각 층의 가중치
            grads['b1']、grads['b2']、... 각 층의 편향
        """
        loss_w = lambda w: self.loss(x, t)

        grads = {}
        for idx in (1, 2, 3):
            grads['W' + str(idx)] = numerical_gradient(loss_w, self.params['W' + str(idx)])
            grads['b' + str(idx)] = numerical_gradient(loss_w, self.params['b' + str(idx)])

        return grads

    def gradient(self, x, t):
        """기울기를 구한다(오차역전파법).

        Parameters
        ----------
        x : 입력 데이터
        t : 정답 레이블

        Returns
        -------
        각 층의 기울기를 담은 사전(dictionary) 변수
            grads['W1']、grads['W2']、... 각 층의 가중치
            grads['b1']、grads['b2']、... 각 층의 편향
        """
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.last_layer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 결과 저장
        grads = {}
        grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
        grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

        return grads
        
    def save_params(self, file_name="params.pkl"):
        params = {}
        for key, val in self.params.items():
            params[key] = val
        with open(file_name, 'wb') as f:
            pickle.dump(params, f)

    def load_params(self, file_name="params.pkl"):
        with open(file_name, 'rb') as f:
            params = pickle.load(f)
        for key, val in params.items():
            self.params[key] = val

        for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
            self.layers[key].W = self.params['W' + str(i+1)]
            self.layers[key].b = self.params['b' + str(i+1)]

7.6 CNN 시각화하기

합성곱 계층을 시각화하여 CNN이 보고 있는 것이 무엇인지 알아보자

7.6.1 1번째 층의 가중치 시각화하기

앞의 MNIST 데이터셋에서 CNN 학습의 1번째 층 합성곱 계층의 가중치
(30, 1, 5, 5) = 필터 30개, 채널 1개, 5x5 크기
이 필터를 1채널의 회색조 이미지로 시각화할 수 있음

학습 전, 후의 가중치를 비교해보자

[그림 7-24] 학습 전과 후의 1번째 층의 합성곱 계층의 가중치 : 가중치의 원소는 실수이지만, 이미지에서는 가장 작은 값(0)은 검은색, 가장 큰 값(255)은 흰색으로 정규화하여 표시함

학습 전 : 무작위 초기화, 흑백에 규칙성 없음
학습 후 : 규칙성 있는 이미지, 흰-검의 변화하는 필터와 덩어리(블롭)가 진 필터 등, 규칙을 띄는 필터

(소스 코드)

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from simple_convnet import SimpleConvNet

def filter_show(filters, nx=8, margin=3, scale=10):
    """
    c.f. https://gist.github.com/aidiary/07d530d5e08011832b12#file-draw_weight-py
    """
    FN, C, FH, FW = filters.shape
    ny = int(np.ceil(FN / nx))

    fig = plt.figure()
    fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)

    for i in range(FN):
        ax = fig.add_subplot(ny, nx, i+1, xticks=[], yticks=[])
        ax.imshow(filters[i, 0], cmap=plt.cm.gray_r, interpolation='nearest')
    plt.show()


network = SimpleConvNet()
# 무작위(랜덤) 초기화 후의 가중치
filter_show(network.params['W1'])

# 학습된 가중치
network.load_params("params.pkl")
filter_show(network.params['W1'])

[그림 7-25] 가로 에지오 ㅏ세로 에지에 반응하는 필터 : 출력 이미지 1은 세로 에지에 흰 픽셀이 나타나고, 출력 이미지 2는 가로 에지에 흰 픽셀이 많이 나온다.

규칙성이 있는 필터는 에지(색상이 바뀐 경계선)와 블롭(국소적으로 덩어리진 영역) 등을 보고 있음

ex) 왼쪽 절반이 흰색 나머지는 검은색 = 세로 방향 에지에 반응하는 필터

이처럼 합성곱 계층의 필터는 에지나 블롭 등의 원시적인 정보를 추출

이를 뒷단 계층에 전달하는 것이 앞서 구현한 CNN의 과업

7.6.2 층 깊이에 따른 추출 정보 변화

1번째 층의 합성곱 계층에서는 에지나 블롭 등의이 저수준 정보 추출
계층이 깊어질수록 추출되는 정보(정확히는 강하게 반응하는 뉴런)는 더 추상화됨

[그림 7-26] CNN의 합성곱 계층에서 추출되는 정보. 1번째 츠은 에지와 블롭, 3번째 층은 텍스처, 5번째 층은 사물의 일부, 마지막 완전연결 계층은 사물의 클래스(개, 자동차)에 뉴런이 반응

층이 깊어지면서 뉴런이 반응하는 대상이 단순한 모양에서 '고급' 정보로 변화
사물의 '의미'를 이해하도록 변화하는 것

7.7 대표적인 CNN

두 네트워크를 살펴보자

CNN의 원소인 LeNet, 딥러닝이 주목받도록 이끈 AlexNet

7.7.1 LeNet

손글씨 숫자를 인식하는 네트워크, 1998년 제안

합성곱 계층과 풀링 계층(정확히는 단순히 '원소를 줄이기'만 하는 서브샘플링 계층)을 반복
마지막으로 완전연결 계층을 거치면서 결과 출력

'현재의 CNN'과의 차이점

활성화 함수 :LeNet은 시그모이드 함수 사용, 현재는 주로 ReLU
풀링 : LeNet은 서브샘플링으로 중간 데이터 크기 줄임, 현재는 최대 풀링이 주류

7.7.2 AlexNet

합성곱 계층과 풀링 게층을 거듭하며 마지막으로 완전연결 계층을 거쳐 결과 출력

LeNet에서 큰 구조는 바뀌지 않았지만, 다음과 같은 변화

활성화 함수로 ReLU 사용
LRN(Local Response Normalization)이라는 국소적 정규화를 실시하는 계층 이용
드롭아웃 사용

그리고 환경과 컴퓨터 기술이 큰 진보를 이룸

특히 GPU가 보급되며 대량의 연산을 고속으로 수행할 수 있게 됨

* NOTE

딥러닝(심층 신경망)에는 대부분 수많은 매개변수가 쓰임
학습하려면 엄청난 양의 게산을 해야함
매개변수 피팅시키는 데이터도 대량으로 필요

→ GPU와 빅데이터로 해결

7.8 정리

CNN은 지금까지의 완전연결 계층 네트워크에 합성곱 계층과 풀링 계층을 새로 추가한다.
합성곱 계층과 풀링 계층은 im2col (이미지를 행렬로 전개하는 함수)을 이용하면 간단하고 효율적으로 구현할 수 있다.
CNN을 시각화해보면 계층이 깊어질수록 고급 정보가 추출되는 모습을 확인할 수 있다.
대표적인 CNN에는 LeNet과 AlexNet이 있다.
딥러닝의 발전에는 빅 데이터와 GPU가 크게 기여했다.