[프레임워크 기초] 제1고지. 미분 자동 계산
Intro
책의 다섯가지 고지와 정복하고자 하는 목표

현재 만들고 있는 클래스가 전체 구조에서 어디에 위치하는지 or 다른 클래스와의 관계가 궁금할 때 참고!

DeZero
- 이 책의 오리지널 프레임워크
- 체이너를 기초로 파이토치의 설계를 덧씌움
1. 상자로서의 변수
1.1 변수란

- 상자는 데이터와 별개
- 상자에는 데이터가 들어감 (대입 or 할당)
- 상자 속을 들여다보면 데이터 알 수 있음 (참조)
1.2 Variable 클래스 구현
변수는 영어로 variable
- DeZero에서 사용하는 변수 개념을 Variable 이름의 클래스로 구현
- 파이썬은 클래스 이름 첫 글자 보통 대문자
* cf : 파이썬이 권장하는 코딩 규칙
https://peps.python.org/pep-0008/
PEP 8 – Style Guide for Python Code | peps.python.org
PEP 8 – Style Guide for Python Code Author: Guido van Rossum , Barry Warsaw , Alyssa Coghlan Status: Active Type: Process Created: 05-Jul-2001 Post-History: 05-Jul-2001, 01-Aug-2013 Table of Contents This document gives coding conventions for the Python
peps.python.org
class Variable:
def __init__(self, data):
self.data = data- 초기화 함수 __init__에 주어진 인수를 인스턴스 변수 data에 대입
- Variable 클래스를 상자로 사용할 수 있음
- 실제 데이터가 Variable의 data에 보관
import numpy as np
data = np.array(1.0)
x = Variable(data)
print(x.data)
>>> 1- 상자에 넣는 데이터 : 넘파이의 다차원 배열
- x : Variable 인스턴스, 데이터를 담은 상자
x.data = np.array(2.0)
print(x.data)
>>> 2.0- x.data = ... 형태로 쓰면 새로운 데이터 대입
1.3 [보충] 넘파이의 다차원 배열
넘파이의 다차원 배열
- 숫자 등의 원소가 일정하게 모여 있는 데이터 구조
- 원소의 순서에는 방향이 있음 → 차원(dimension) or 축(axis)

- 스칼라 : 단순히 하나의 수
- 벡터 : 하나의 축을 따라 숫자가 늘어섬
- 행렬 : 축이 두 개
* NOTE
- 텐서 : 다차원 배열
- 스칼라 = 0차원 텐서
- 벡터 = 1차원 텐서
- 행렬 = 2차원 텐서
import numpy as np
x = np.array(1)
x.ndim
>>> 0
x = np.array([1, 2, 3])
x.ndim
>>> 1
x = np.array([[1, 2, 3],
[4, 5, 6]])
x.ndim
>>> 2- 넘파이 ndarray 인스턴스의 ndim 인스턴스 변수
- ndim = number of dimensions = 다차원 배열의 차원 수
* CAUTION : 차원
- 벡터의 차원 : 벡터의 원소 수
- 3차원 배열 = (원소가 아닌) 축이 3개
- np.array([1, 2, 3]) = 3차원 벡터
2. 변수를 낳는 함수
2.1 함수란
어떤 변수로부터 다른 변수로의 대응 관계를 정한 것

- 변수 : x, y
- 함수 : f
- 계산 그래프 : 변수 ○, 함수 □ 모양의 노드들을 화살표로 연결해 계산 과정을 표현한 그림
2.2 Function 클래스 구현
Variable 인스턴스를 변수로 다룰 수 있는 함수를 Function 클래스로 구현
- Function 클래스는 Variable 인스턴스를 입력받아 Variable 인스턴스 출력
- Variable 인스턴스의 실제 데이터는 인스턴스 변수인 data에 있음
class Function:
def __call__(self, input):
x = input.data # 데이터를 꺼낸다.
y = x ** 2 # 실제 계산
output = Variable(y) # Variable 형태로 되돌린다.
return output- __call__ 메서드의 인수 input은 Variable 인스턴스라고 가정
- 실제 데이터는 input.data에 존재
- 데이터를 꺼낸 후 원하는 계산(제곱)을 하고, 결과를 Variable이라는 '상자'에 담아 돌려줌
* NOTE : __call__ 메서드
- 파이썬의 특수 메서드
- 이 메서드를 정의하면 f = Function() 형태로 함수의 인스턴스를 변수 f에 대입해두고,
- 나중에 f(...)형태로 __call__ 메서드 호출할 수 있음
2.3 Function 클래스 이용
x = Variable(np.array(10))
f = Function()
y = f(x)
print(type(y)) # type() 함수는 객체의 클래스를 알려준다.
print(y.data)
>>> <class '__main__.Variable'>
>>> 100- Variable 인스턴스인 x를 Function 인스턴스인 f에 입력
- Variable과 Function을 연계할 수 있음
- y의 클래스는 Variable
- 데이터는 y.data에 잘 저장됨
Function 클래스 말고 더 명확한 이름을 붙이자
- Function 클래스는 기반 클래스로서, 모든 함수에 공통되는 기능을 구현
- 구체적인 함수는 Function 클래스를 상속한 클래스에서 구현
class function:
def __call__(self, input):
x = input.data
y = self.forward(x) # 구체적인 계산은 forward 메서드에서 한다.
output = Variable(y)
return output
def forward(self, x):
raise NotImplementedError()
수정된 코드
- __call__ : 'Variable에서 데이터 찾기', '계산 결과를 Variable에 포장하기' 수행
- forward : 구체적인 로직을 하위 클래스에서 구현
* NOTE
- Function 클래스의 forward 메서드는 예외 발생
→ '이 메서드는 상속하여 구현해야 한다'는 사실을 알려주기 위해
class Square(Function):
def forward(self, x):
return x ** 2
Square 클래스는 Function 클래스를 상속하기 때문에 __call__ 메서드는 그대로 계승
- forward 메서드에 구체적인 계산 로직 작성하여 구현 끝
x = Variable(np.array(10))
f = Square()
y = f(x)
print(type(y))
print(y.data)
>>> <class '__main__.Variable'>
>>> 100
3. 함수 연결
또 다른 함수를 구현하고 여러 함수를 조합해 계산하자
3.1 Exp 함수 구현
y = e^x 를 계산하는 함수 (* e ≒ 2.718...)
class Exp(Function):
def forward(self, x):
return np.exp(x)- Square 클래스와 마찬가지로 Function 클래스 상속
- forward 메서드에서 원하는 계산 구현
3.2 함수 연결
Function 클래스의 __call__ 메서드는 입력과 출력이 모두 Variable 인스턴스
- DeZero 함수들을 연이어 사용할 수 있음
A = Squrare()
B = Exp()
C = Squrare()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
y = C(b)
print(y.data)
>>> 1.648721270700128- 3개의 함수 A, B, C를 연이어 적용
- 중요 : 중간에 4개의 변수 x, a, b, y가 모두 Variable 인스턴스
- Function 클래스의 __call__ 메서드의 입출력이 Variable 인스턴스로 통일 → 여러 함수 연속 적용 가능

* NOTE : 합성 함수(composite function)
- 여러 함수를 순서대로 적용하여 만들어진 변환 전체를 하나의 큰 함수로 보는 것
- 각 함수를 연속으로 적용하면 복잡한 계산도 해낼 수 있음
계산 그래프를 이용하면 각 변수에 대한 미분을 효율적으로 계산할 수 있음
4. 수치 미분
미분을 자동으로 계산하기 위해 Variable, Function 클래스를 구현
4.1 미분이란
미분 = '변화율' = '극한으로 짧은 시간'에서의 변화량

- lim는 h가 한없이 0에 근접한다는 뜻
- 오른쪽 식 부분은 [그림 4-1]과 같이 두 점을 지나는 직선의 기울기
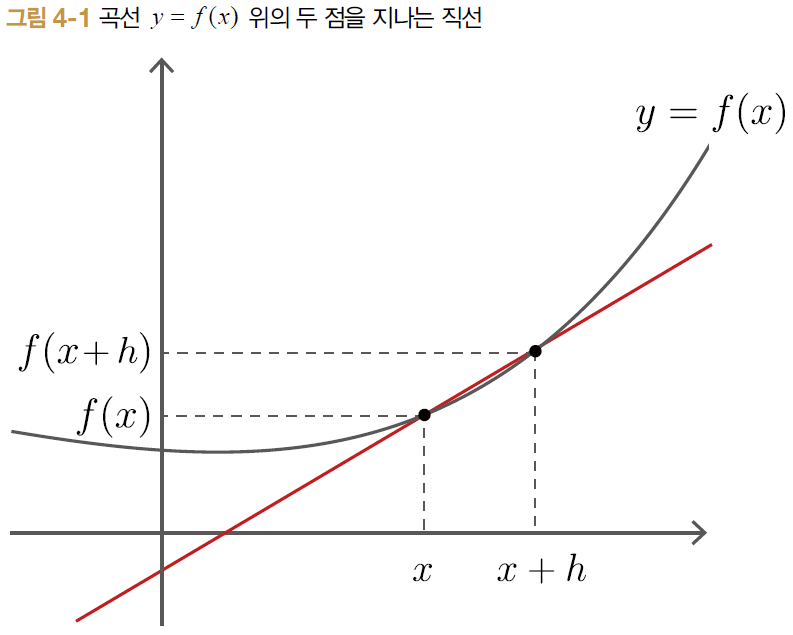
- h를 한없이 0에 가깝게 줄여 x의 변화 비율을 구하면 값이 y = f(x)의 미분
- y = f(x) 가 어떤 구간에서 미분 가능하다면 [식 4.1]은 해당 구간의 '모든 x'에서 성립
- f'(x)도 함수이며, f(x)의 도함수라고 함
4.2 수치 미분 구현
- 컴퓨터는 극한을 취급할 수 없으니 h를 극한과 비슷한 값으로 대체
- 수치미분 : h=0.0001(=1e-1) 와 같은 미세한 차이를 이용하여 함수의 변화량 구하는 것
- 수치 미분은 어쩔 수 없이 근사 오차, 이를 줄이기 위해 '중앙차분'
→ f(x), f(x+h) 대신 f(x-h), f(x+h)의 차이 구함, 상대적으로 오차 작음
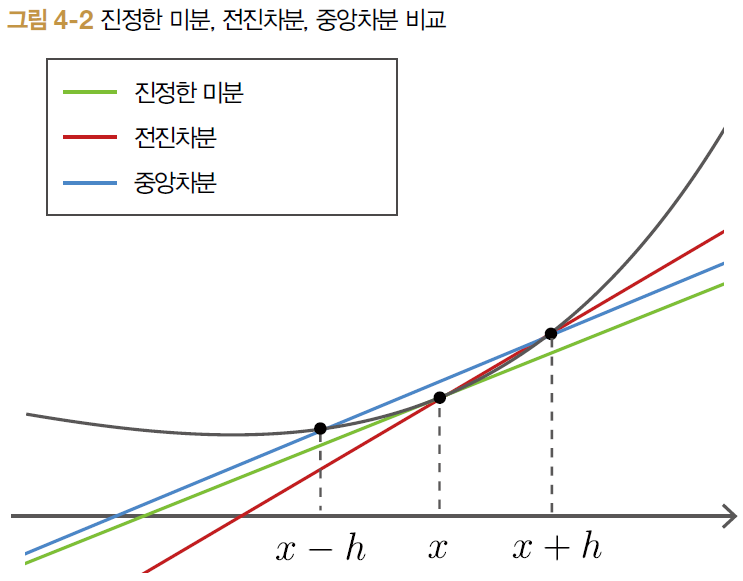
# 중앙차분을 이용하여 수치 미분을 계산하는 함수
def numerical_diff(f, x, eps=1e-4):
x0 = Variable(x.data - eps)
x1 = Variable(x.data + eps)
y0 = f(x0)
y1 = f(x1)
return (y1.data - y0.data) / (2 * eps)- f : 미분의 대상 함수, Funcrion의 인스턴스
- x : 미분을 계산하는 변수, Variable 인스턴스
- eps : 작은값, 1e-4
# 위 코드 수행
f = Square()
x = Variable(np.array(2.0)
dy = numerical_diff(f, x)
print(dy)
>>> 4.000000000004
4.3 합성 함수의 미분
합성 함수 y = (e^(x^2))^2 에 대한 미분 dy/dx 를 계산하는 코드
def f(x):
A = Square()
B = Exp()
C = Square()
return X(B(A(x)))
x = Variable(np.array(0.5))
dy = numerical_diff(f, x)
print(dy)
>>> 3.297442629330694- 실행 결과 3.297 → x를 0.5에서 작은 값만큼 변화시키면 y는 작은 값의 3.297...배만큼 변한다는 의미
- 미분을 '자동으로' 계산하는 코드를 작성
4.4 수치 미분의 문제점
1. 수치 미분의 결과에는 오차 포함
* NOTE : 자릿수 누락
- 중앙차분 등 '차이'를 구하는 계산은, 주로 크기가 비슷한 값들을 다루므로 자릿수 누락
- 유효 자릿수가 줄어들 수 있음
- ex) 0.001434 에서 0.001 로 바뀐 경우
2. 수치 미분은 계산량이 많음
- 변수가 여러 개인 계산을 미분할 경우, 변수 각각을 미분해야 함
- 수백만 개 매개변수를 모두 수치 미분으로 구하는 것은 비현실적
→ 역전파의 등장
수치 미분은 구현 쉽고 정확하지만, 역전파는 복잡한 알고리즘의 버그
- 역전파 구현을 확인하기 위해 수치 미분의 결과 이용 = 기울기 확인(gradient checking)
5. 역전파 이론
- 수치 미분은 계산 비용 & 정확도 문제
- 역전파(backpropagation)은 미분 효율적 계산, 결괏값 오차 작음
5.1 연쇄 법칙
연쇄 법칙(chain rule)
- 여러 함수를 사슬처럼 연결하여 사용하는 모습
- 합성 함수(여러 함수가 연결된 함수)의 미분 == 구성 함수 각각을 미분한 후 곱한 것

ex) y = F(x) 함수는 다음의 세 함수로 구성
- a = A(x)
- b = B(a)
- y = C(b)
x에 대한 y의 미분

- x에 대한 y의 미분은 구성 함수 각각의 미분값을 모두 곱한 값과 동일
- 합성 함수의 미분은 각 함수의 국소적인 미분들로 분해할 수 있음 = 연쇄법칙

- [식 5.1]을 [식 5.2]와 같이 표현할 수도 있음
* NOTE
- dy/dy 는 y의 y에 대한 미분, 항상 1
5.2 역전파 원리 도출

- [식 5.2] : 합성 함수의 미분은 구성 함수들의 미분의 곱으로 분해할 수 있음
- [식 5.3] : 출력에서 입력 방향으로 (즉, 역방향으로) 순서대로 계산

- 출력 y 에서 입력 x 방향으로 곱하면서 순서대로 미분하면 최종적으로 dy/dx 구해짐


- ex) dy/db 는 함수 y = C(b)의 미분 = C'(b) → 함수 C의 도함수를 C'으로 나타낼 수 있음
'y의 각 변수에 대한 미분값', 즉 변수 y, b, a, x에 대한 미분값이 오른쪽에서 왼쪽으로 전파
= 역전파
(중요!) 전파되는 데이터는 모두 'y의 OO에 대한 미분값' (dy/dy, dy/db, dy/da, dy/dx)
* NOTE : [식 5.3]과 같이 계산 순서를 출력에서 입력 방향으로 정한 이유
- y의 미분값 전파를 위해
= y를 '중요 요소'로 대우하기 때문에 - 입력에서 출력 방향으로 계산하면 중요 요소 입력 x가 됨
- (dx/dx → da/dx → db/dx → dy/dx)
- x에 대한 미분을 전파
머신러닝은 주로 대량의 매개변수를 입력받아 마지막에 손실 함수(loss function)을 거쳐 출력
- 손실 함수의 출력은 (많은 경우) 단일한 스칼라값 → 중요 요소
- 손실 함수의 각 매개변수에 대한 미분 계산해야 함
- 미분값을 출력에서 입력 방향으로 전파하면 한 번의 전파만으로 모든 매개변수에 대한 미분 계산
→ 미분을 반대방향으로 전파하는 방식(역전파) 이용
5.3 계산 그래프로 살펴보기

순전파와 역전파 상의 관계
ex)
- 순전파 변수 a와 역전파 미분 dy/da 서로 대응 ...
- 함수 B는 역전파 B'(a)에 대응 ...
→ 변수는 '통상값'과 '미분값' 존재
→ 함수는 '통산 계산(순전파)'과 '미분값을 구하기 위한 계산(역전파)'이 존재
ex)
- [그림 5-5]의 함수 노드 C'(b)는 y = C(b) 계산의 미분
- C'(b)를 계산하려면 b값 필요 ...
→ 역전파 시에는 순전파 시 이용한 데이터가 필요
→ 역전파를 구현하려면 먼저 순전파를 하고, 각 함수 입력 변수(ex. x, a, b) 값을 기억
→ 이후 각 함수의 역전파 계산
6. 수동 역전파
Variable과 Function 클래스를 확장하여 역전파를 이용한 미분 구현
6.1 Variable 클래스 추가 구현
class Variable:
def __init__(self, data):
self.data = data
#####
self.grad = None
#####- grad라는 인스턴스 변수 추가
(기울기 gradient 라는 의미) - 인스턴스 변수 data & grad는 모두 넘파이의 다차원 배열이라 가정
- grad는 None으로 초기화 → 후에 역전파를 하면 미분값을 계산하여 대입
6.2 Function 클래스 추가 구현
이전 Function 클래스는 순전파(forward 메서드) 기능만 지원
다음의 기능을 추가
- 미분을 계산하는 역전파 (backward 메서드)
- forward 메서드 호출 시 건네받은 Variable 인스턴스 유지
class Function:
def __call__(self, input):
x = input.data
y = self.forward
output = Variable(y)
#####
self.input = input # 입력 변수를 기억(보관)한다.
#####
return output
def forward(self, x):
raise NotImplementedError()
#####
def backward(self, gy):
raise NotImplementedError()
#####- __call__ 메서드에서 입력된 input을 인스턴스 변수인 self.input에 저장
- backward 메서드에서 함수(Function)에 입력한 변수(Variable 인스턴스)가 필요할 때 self.input에서 가져와 사용
6.3 Square와 Exp 클래스 추가 구현
Function을 상속한 구체적인 함수에서 역전파(backward) 구현
# 제곱을 계산하는 클래스
class Square(Function):
def forward(self, x):
y = x ** 2
return y
def backward(self, gy):
x = self.input.data
gx = 2 * x * gy
return gx- y = x^2의 미분은 2x이므로 위처럼 구현
- gy : ndarray 인스턴스, 출력 쪽에서 전해지는 미분값 전달하는 역할
- gy에 'y = x^2의 미분'을 곱한 값이 backward의 결과
# y = e^x 계산하는 클래스
class Exp(Function):
def forward(self, x):
y = np.exp(x)
return y
def backward(self, gy):
x = self.input.data
gx = np.exp(x) * gy
return gx- y = e^x의 미분은 e^x이므로 위처럼 구현
6.4 역전파 구현
[그림 6-1]에 해당하는 계산의 미분을 역전파로 계산
순전파

# 순전파 코드
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
y = C(b)
역전파
- 순전파 때와 반대 순서로 각 함수의 backward 메서드 호출
- 역전파는 dy/dy = 1에서 시작
- 이후 C - B - A 순으로 backward 메서드 호출 = 각 변수의 미분값

y.grad = np.array(1.0)
b.grad = C.backward(y.grad)
a.grad = B.backward(b.grad)
x.grad = A.backward(a.grad)
print(x.grad)
7. 역전파 자동화
그러나 역전파 순서(C - B - A) 호출이 불편하니, 자동화해보자.
역전파 자동화
- 일반적인 계산(순전파)를 한 번만 하면 역전파 자동으로 이루어지는 구조
- Define-by-Run의 핵심

* NOTE : Define-by-Run
- '동적 계산 그래프'
- 딥러닝에서 수행하는 계산들을 계산 시점에 '연결'하는 방식
7.1 역전파 자동화의 시작
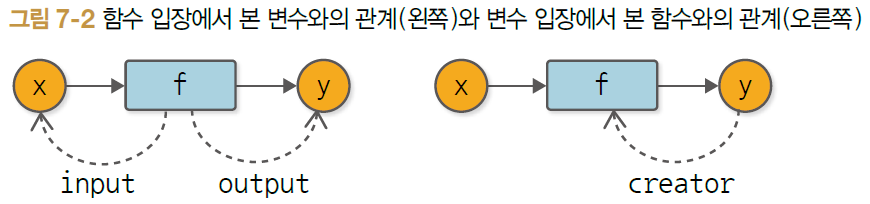
역전파 자동화는 변수와 함수의 '관계' 이해에서 출발
- 변수는 함수에 의해 '만들어짐'
= 변수에게 함수는 '창조자(creater)' or '부모' - 창조자인 함수가 존재하지 않는 변수는, 사용자에 의해 만들어진 변수로 간주
class Variable:
def __init__(self, data):
self.data = data
self.grad = None
#####
self.creaator = None
#####
#####
def set_creator(self, func):
self.creator = func
#####- 일반적인 계산(순전파)이 이루어지는 시점에 '관계'를 맺어주도록(함수, 변수 연결) 만듦
- creator 변수추가
- creator 설정을 위해 set_creator 메서드 추가
class Function:
def __call__(self, data):
x = input.data
y = self.forward(x)
output = Variable(y)
output.set_creator(self) # # 출력 변수에 창조자를 설정
self.input = input
self.output = output # # 출력도 저장
return output- 순전파 계산하면 결과로 output이라는 Variable 인스턴스 생성
- 생성된 output에 '내가 너의 창조자임'을 기억시킴 → '연결'을 동적으로 만드는 기법 핵심
- output을 인스턴스 변수에 저장
* NOTE
- DeZero의 동적 계산 그래프는 실제 계산이 이루어질 때 변수(상자)에 관련 '연결'을 기록
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
y = C(b)
# 계산 그래프의 노드들을 거꾸러 거슬러 올라간다.
assert y.creator == C
assert y.creator.input == b
assert y.creator.input.creator == B
assert y.creator.input.creator.input == a
assert y.creator.input.creator.input.creator == A
assert y.creator.input.creator.input.creator.input == x
assert
- '단호하게 주장하다', '단언하다'
- 평가 결과가 True가 아니면 예외 발생
- 조건 충족 여부를 확인하는 데 사용
- 앞 코드는 문제 없이 실행되므로 assert문의 조건 모두 충족
계산 그래프가 함수와 변수 사이 연결로 구성
- '연결'이 실제로 계산을 수행하는 시점(순전파에 데이터 흘려보낼 때) 만들어짐
= Define-by-Run (데이터를 흘려보냄으로써 연결이 규정됨) - '링크드 리스트' 데이터 구조를 이용해 계산 그래프 표현
- 노드 : 그래프 구성 요소
- 링크 : 다른 노드를 가리키는 참조

7.2 역전파 도전!

이 계산 그래프를 순서대로 구현
# y에서 b까지의 역전파
y.grad = np.array(1.0)
C = y.creator # 1. 함수를 가져온다.
b = C.input # 2. 함수의 입력을 가져온다.
b.grad = C.backward(y.grad) # 3. 함수의 backward 메서드를 호출한다.
# b에서 a로의 역전파
B = b.creator # 1. 함수를 가져온다.
a = B.input # 2. 함수의 입력을 가져온다.
a.grad = B.backward(b.grad) # 3. 함수의 backward 메서드를 호출한다.
# a에서 x로의 역전파
A = a.creator # 1. 함수를 가져온다.
x = A.input # 2. 함수의 입력을 가져온다.
x.grad = A.backward(a.grad) # 3. 함수의 backward 메서드를 호출한다.
print(x.grad)
>>> 3.297442541400256
모든 역전파 끝
7.3 backwaard 메서드 추가
앞 역전파 코드의 반복 작업 자동화
→ Variable 클래스에 backward라는 새로운 메서드 추가
class Variable:
def __init__(self, data):
self.data = data
self.grad = None
self.creator = None
def set_creator(self, func):
self.creator = func
def backward(self):
f = self.creator # 1. 함수를 가져온다.
if f is not None:
x = f.input # 2. 함수의 입력을 가져온다.
x.grad = f.backward(self.grad) # 3. 함수의 backward 메서드를 호출한다.
x.backward() # 하나 앞 변수의 backward 메서드를 호출한다(재귀)- Variable의 creator에서 함수를 얻어오고, 그 함수의 입력 변수를 가져옴
- backward 메서드 호출
- 자신보다 하나 앞에 놓인 변수의 backward 메서드 호출
=> 각 변수의 backward 메서드가 재귀적으로 불림
* NOTE
- Variable 인스턴스의 creator가 None이면 역전파 중단
= 창조자가 없으므로 이 Variable 인스턴스는 함수 바깥에서 생성됐음(높은 확률로 사용자가 건넨 변수)
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
y = C(b)
# backward
y.grad = np.array(1.0)
y.backward()
print(x.grad)- 변수 y의 backward 메서드를 호출하면 역전파가 자동으로 진행
- DeZero의 가장 중요한 자동 미분의 기초 완성
(7절 전체 코드)
import numpy as np
class Variable:
def __init__(self, data):
self.data = data
self.grad = None
self.creator = None
def set_creator(self, func):
self.creator = func
def backward(self):
f = self.creator # 1. Get a function
if f is not None:
x = f.input # 2. Get the function's input
x.grad = f.backward(self.grad) # 3. Call the function's backward
x.backward()
class Function:
def __call__(self, input):
x = input.data
y = self.forward(x)
output = Variable(y)
output.set_creator(self) # Set parent(function)
self.input = input
self.output = output # Set output
return output
def forward(self, x):
raise NotImplementedError()
def backward(self, gy):
raise NotImplementedError()
class Square(Function):
def forward(self, x):
y = x ** 2
return y
def backward(self, gy):
x = self.input.data
gx = 2 * x * gy
return gx
class Exp(Function):
def forward(self, x):
y = np.exp(x)
return y
def backward(self, gy):
x = self.input.data
gx = np.exp(x) * gy
return gx
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
y = C(b)
# backward
y.grad = np.array(1.0)
y.backward()
print(x.grad)
8. 재귀에서 반복문으로
처리 효율을 개선하고, 확장을 대비해 backward 메서드 구현 방식을 바꿔보자.
8.1 현재의 Variable 클래스
class Variable:
... # 생략
def backward(self):
f = self.creator # 1. Get a function
if f is not None:
x = f.input # 2. Get the function's input
x.grad = f.backward(self.grad) # 3. Call the function's backward
x.backward()
문제
- 하나 앞 변수의 backward 메서드 호출 코드 → 재귀 구조
8.2 반복문을 이용한 구현
'재귀를 사용한 구현' → '반복문을 이용한 구현'으로 고쳐보자
class Variable:
... # 생략
def backward(self):
func = [self.creator]
while funcs:
f = funcs.pop() # 함수를 가져온다.
x, y = f.input, f.output # 함수의 입력과 출력을 가져온다.
x.grad = f.backward(y.grad) # backward 메서드를 호출한다.
if x.creator in not None:
funcs.append(x.creator) # 하나 앞의 함수를 리스트에 추가한다.- 처리해야 할 함수들을 funcs 리스트에 차례로 집어넣음
- while 블록 안에서 funcs.pop()을 호출하여 처리할 함수 f 꺼냄, f의 backward 메서드 호출
- f.input과 f.output에서 함수 f의 입력과 출력 변수를 얻음으로써 f.backward()의 인수와 반환값을 올바르게 설정
* NOTE : pop 메서드
- 리스트에서 마지막 원소를 꺼내줌
8.3 동작 확인
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
y = C(b)
# backward
y.grad = np.array(1.0)
y.backward()
print(x.grad)
>>>< 3.297442541400256- 결과는 이전과 동일
- '재귀'에서 '반복문'으로 구현 방식 전환
→ 15단계에서 이 방식의 이점 : 복잡한 계산 그래프에서 부드럽게 확장 가능, 처리 효율도 반복문 방식이 뛰어남
* 재귀
- 함수를 재귀적으로 호출할 때마다 중간 결과를 메모리에 유지하면서 처리 이어감
→ 반복문이 효율 더 좋음
9. 함수를 더 편리하게
- DeZero가 역전파 & Define-by-Run 전체 계산의 각 조각들을 런타임에 '연결' 능력 갖춤.
- 사용자 편의성을 높이기 위해 DeZero 함수에 세 가지 개선 추가
9.1 파이썬 함수로 이용하기
# 문제의 코드
x = Variable(np.array(0.5))
f = Square()
y = f(x)- Square 클래스의 인스턴스를 생성한 다음, 이어서 그 인스턴스를 호출하는 두 단계로 구분해 진행
→ 사용자 입장에서 번거로움 - y = Square() (x) 형태로 적을 수도 있지만, 모양새 좋지 않음
=> '파이썬 함수'를 지원!
# 해결 코드 1
def square(x):
f = Square()
return f(x)
def exp(x):
f = Exp()
return f(x)# 해결 코드2
def square(x):
return Square()(x)
def exp(x):
return Exp()(x)
최초의 np.array(0.5)를 Variable로 감싸면 일반적인 수치 계산을 하듯, 넘파이를 사용해 계산 가능
- 함수를 연속으로 적용할 수 있음
- 둘은 동일한 코드
수정한 코드
x = Variable(np.array(0.5))
y = square(exp(square(x))) # 연속하여 적용
y.grad = np.array(1.0)
y.backward()
print(x.grad)
>>> 3. 297442541400256
9.2 backward 메서드 간소화
- 역전파 시 사용자의 번거로움을 줄여보자
y.grad = np.array(1.0) 부분 생략하도록 코드 수정
class Variable:
...
def backward(self):
if self.grad is None: #
self.grad = np.ones_like(self.data) #
funcs = [self.creator]
while funcs:
f = funcs.pop()
x, y = f.input, f.output
x.grad = f.backward(y.grad)
if x.creator is not None:
funcs.append(x.creator)- 만약 변수의 grad가 None이면 자동으로 미분값 생성
- np.ones_like(self.data)
- self.data와 형상과 데이터 타입이 같은 ndarray 인스턴스를 생성하는데, 모든 요소를 1로 채워서 돌려줌
- self.data가 스칼라면 self.grad도 스칼라가 됨
* NOTE : np.array(1.0) 대신 np.ones_like()을 쓴 이유
- Variable의 data와 grad의 데이터 타입을 같게 만들기 위해서
- ex) data의 타입이 32비트 부동소수점 숫자면 grad의 타입도 32비트 부동소수점 숫자가 됨
x = Variable(np.array(0.5))
y = square(exp(square(x)))
y.backward()
print(x.grad)
>>> 3.297442541400256- 최종 출력 변수에서 backward 메서드를 호출하는 것만으로 미분값 구해짐
9.3 ndarray만 취급하기
- DeZero의 Variable은 데이터로 ndarray 인스턴스만 취급하게끔 의도
- 하지만 float나 int 같은 의도치 않은 데이터 타입을 사용한다면 문제...
- 이를 막기 위해 Variable에 ndarray 인스턴스 외의 데이터를 넣을 경우 즉시 오류 일으키는 코드
class Variable:
def __init__(self, data):
if data is not None: *
if not isinstance(data, np.ndarray): *
raise TypeError('{} is not supported'.format(type(data))) *
self.data = data
self.grad = None
self.creator = None- 인수로 주어진 data가 None도 아니고, ndarray 인스턴스도 아니라면 TypeError 예외 발생
- 출력할 오류 메시지도 준비
변경된 코드 사용 결과
x = Variable(np.array(1.0)) # OK
x = Variable(None) # OK
x = Variable(1.0) # NG
>>> TypeError : <class 'float'> is not supported.
이렇게 바꾸었을 때, 넘파이의 독특한 관례로 인한 주의할 점
# 문제 없음
x = np.array([1.0])
y = x ** 2
print(type(x), x.ndim)
print(type(y))
# 실행결과
<class 'numpy.ndarry'> 1
<class 'numpy.ndarry'># 문제 있음
x = np.array(1, 0)
y = x ** 2
print(type(x), x.ndim)
print(type(y))
# 실행결과
<class 'numpy.ndarry'> 0
<class 'numpy.float64'>- x는 0차원의 ndarray
- 제곱(x**2)을 하면 np.float64가 되어버림
→ 0차원 ndarray 인스턴스를 사용하면 계산 결과 데이터 타입이 달라짐
def as_array(x):
if np.isscalar(x):
return np.array(x)
return x- np.isscalar는 입력 데이터가 numpy.float64와 같은 스칼라 타입(파이썬 int, float)인지 확인해주는 함수
- as_array는 입력을 ndarray 인스턴스로 변환
Function 클래스에 as_array 편의 함수 추가
class Function:
def __call__(self, input):
x = input.data
y = self.forward(x)
output = Variable(as_array(y)) *
output.set_creator(self)
self.input = input
self.output = output
return output- 순전파의 결과인 y를 Variable로 감쌀 때 as_array() 이용
- output은 항상 ndarray 인스턴스가 되도록 보장
(전체 코드)
import numpy as np
class Variable:
def __init__(self, data):
if data is not None:
if not isinstance(data, np.ndarray):
raise TypeError('{} is not supported'.format(type(data)))
self.data = data
self.grad = None
self.creator = None
def set_creator(self, func):
self.creator = func
def backward(self):
if self.grad is None:
self.grad = np.ones_like(self.data)
funcs = [self.creator]
while funcs:
f = funcs.pop()
x, y = f.input, f.output
x.grad = f.backward(y.grad)
if x.creator is not None:
funcs.append(x.creator)
def as_array(x):
if np.isscalar(x):
return np.array(x)
return x
class Function:
def __call__(self, input):
x = input.data
y = self.forward(x)
output = Variable(as_array(y))
output.set_creator(self)
self.input = input
self.output = output
return output
def forward(self, x):
raise NotImplementedError()
def backward(self, gy):
raise NotImplementedError()
class Square(Function):
def forward(self, x):
y = x ** 2
return y
def backward(self, gy):
x = self.input.data
gx = 2 * x * gy
return gx
class Exp(Function):
def forward(self, x):
y = np.exp(x)
return y
def backward(self, gy):
x = self.input.data
gx = np.exp(x) * gy
return gx
def square(x):
return Square()(x)
def exp(x):
return Exp()(x)
x = Variable(np.array(0.5))
y = square(exp(square(x)))
y.backward()
print(x.grad)
x = Variable(np.array(1.0)) # OK
x = Variable(None) # OK
x = Variable(1.0) # NG
10. 테스트
- SW개발에서 테스트의 중요성
- 딥러닝 프레임워크의 테스트 방법에 대해 알아보자
10.1 파이썬 단위 테스트
파이썬으로 테스트할 때는 표준 라이브러리에 포함된 unittest 사용
이전 단계에서 구현한 square 함수 테스트
import unittest
class SquareTest(unittest.TestCase):
def test_forward(self):
x = Variable(np.array(2.0))
y = square(x)
expected = np.array(4.0)
self.assertEqual(y.data, expected)- unittest를 임포트하고 unittest.TestCase를 상속한 SquareTest 클래스를 구현
- square 함수의 출력이 기댓값과 같은지 확인
- 입력이 2.0일 때 출력이 4.0이 맞는지 확인
* 규칙
- 테스트할 때는 이름이 test로 시작하는 메서드 만들고, 그 안에 테스트할 내용을 적음
* NOTE : self.assertEqual
- 주어진 두 객체가 동일한지 여부를 판정
- cf) 그 밖에도 self.assertGreater, self.assertTrue 등 unittest에 다양한 메서드 준비되어 있음 (unittest 문서 참고)
# 터미널에서 테스트
python -m unittest steps/step10.py- -m unittest 인수를 제공하면 파이썬 파일을 테스트 모드로 실행할 수 있음
(전체 코드)
import unittest
class SquareTest(unittest.TestCase):
def test_forward(self):
x = Variable(np.array(2.0))
y = square(x)
expected = np.array(4.0)
self.assertEqual(y.data, expected)
def test_backward(self):
x = Variable(np.array(3.0))
y = square(x)
y.backward()
expected = np.array(6.0)
self.assertEqual(x.grad, expected)
def test_gradient_check(self):
x = Variable(np.random.rand(1))
y = square(x)
y.backward()
num_grad = numerical_diff(square, x)
flg = np.allclose(x.grad, num_grad)
self.assertTrue(flg)
10.2 square 함수의 역전파 테스트
import unittest
class SquareTest(unittest.TestCase):
...
def test_backward(self):
x = Variable(np.array(3.0))
y = square(x)
y.backward()
expected = np.array(6.0)
self.assertEqual(x.grad, expected)- y.backward()로 미분값을 구하고, 그 값이 기댓값과 일치하는지 확인
- 기댓값 6.0은 계산해서 구한 값을 하드코딩한 것
10.3 기울기 확인을 이용한 자동 테스트
- 앞 절에서 미분의 기댓값 손으로 계산해 입력
기울기 확인
- 이 부분을 자동화할 방법
- 수치 미분으로 구한 결과와 역전파로 구한 결과를 비교
- 그 차이가 크면 역전파 구현에 문제가 있다고 판단하는 검증 기법
* NOTE : 수치 미분
- 수치 미분은 쉽게 구현할 수 있음
- 거의 정확한 미분값을 내어줌
→ 수치 미분의 결과와 비교하면 역전파를 정확히 구현했는지 검증 가능
def numerical_diff(f, x, eps=1e-4):
x0 = Variable(x.data - eps)
x1 = Variable(x.data + eps)
y0 = f(x0)
y1 = f(x1)
return (y1.data - y0.data) / (2 * eps)
class SquareTest(unittest.TestCase):
...
def test_gradient_check(self):
x = Variable(np.random.rand(1)) # 무작위 입력값 생성
y = square(x)
y.backward()
num_grad = numerical_diff(square, x)
flg = np.allclose(x.grad, num_grad)
self.assertTrue(flg)- 기울기 확인을 할 test_gradient_check 메서드 안에서 무작위 입력값 하나 생성
- 역전파로 미분값 구함, numerical_diff 함수로 수치 미분 계산
- 두 메서드로 각각 구한 값들이 거의 일치하는지 확인 : np.allclose 넘파이 함수 이용
* np.allclose(a, b)
- 인스턴스 a와 b의 값이 가까운지 판정
- 가까움의 기준은 np.alloclose(a, b, rtol=1e-05, atol=1e-08)과 같이 인수 rtol과 atol로 지정
- 다음 조건을 만족하면 True
| a - b | <= ( atol + rtol * |b| )
10.4 테스트 정리
- 테스트 코드는 tests 디렉터리에 있음
테스트 파일 한꺼번에 실행
python -m unittest discover tests- discover라는 하위 명령을 사용하면 discover 다음에 지정한 디렉터리에 테스트 파일이 있는지 검색(test*.py)
- test 디렉터리에 들어 있는 모든 테스트 한 번에 실행

- DeZero의 깃허브 저장소는 '트래비스 CI'라는 지속적 통합 서비스와 연계
- DeZero의 깃허브 저장소에서 코드를 푸시, 풀 리퀘스트를 병합, 매시간 자동으로 테스트 실행되도록 설정
- 테스트 결과에 문제가 있으면 메일 등으로 보고
- 깃허브 첫 화면에 빌드 상태 표기되게
- build : passing은 빌드 후 테스트까지 통과했다는 표시 → 코드의 신뢰성 유지
칼럼 : 자동 미분
역전파 vs 자동 미분
- 자동 미분은 더 제한적인 방법을 의미하므로 주의
* NOTE : 자동 미분
- 어떤 계산(함수)을 코드로 구현하면 그 계산의 미분을 컴퓨터가 자동으로 계산해주는 시스템
컴퓨터 프로그램에서 미분 계산하는 방법
1. 수치 미분(numerical differentiation)
- 변수에 미세한 차이를 주어 일반적인 계산(순전파)을 2회 실시
- 두 출력의 차이로부터 근사적으로 미분 계산
- 장점 : 구현이 쉬움
- 단점 : 출력에 오차 포함되기 쉬움, 다량의 변수를 사용하는 함수를 다룰 때 계산 비용 높음
2. 기호 미분(symbolic differentiation)
- 미분 공식을 이용하여 계산
- 입력도 '수식' 출력도 '수식
- Mathmatica와 MATLAB 등에서 이용
* CAUTION
- 기호 미분의 출력은 미분된 '식' (즉, 도함수)
- 출력 시점에는 아무런 수치 계산도 수행되지 않음
- 도함수 얻은 후, 구체적인 값에서의 미분 계산
- 단점 : 수식이 크게 부풀어 오르기 쉬움 (특히 최적화 고려하지 않고 구현하면... 수식 폭발)
3. 자동 미분(automatic differentiation)
- 연쇄 법칙을 사용하여 미분하는 방법
- 어떤 함수를 프로그램으로 짜서 건네주면 그 미분을 효율적이고 정밀하게 계산
- 종류 : forward 모드 & revere 모드
- ex) 역전파 방식도 자동 미분(reverse 모드 자동 미분)
* NOTE
- 역전파(reverse 모드 자동 미분)는 미분 결과를 출력 쪽으로부터 입력 쪽으로 전달
- forward 모드 자동 미분은 입력 쪽으로부터 출력 쪽으로 전달
→ 두 방법 모두 연쇄 법칙 사용하여 미분값 계산하지만 '경로'가 다름 - 출력이 하나 뿐이고, 그 하나의 출력 변수를 미분하려면 reverse 모드 자동 미분이 적합
→ 머신러닝은 대부분 출력이 변수 하나로 모아지는 문제 다루므로 reverse 모드 자동 미분 사용

- 딥러닝 프레임워크는 'reverse 모드 자동 미분'을 구현해 사용
- 문헌에 따라 forward 모드와 reverse 모드를 구분하지 않고, 역전파를 가리켜 '자동 미분'이라고 부르기도 함