[NLP 기초] 1. 신경망 복습
1.1 수학과 파이썬 복습
( [AI 기초] 편에 잘 정리되어 있으므로 패스 )
1.1.1 벡터와 행렬
1.1.2 행렬의 원소별 연산
1.1.3 브로드캐스트
1.1.4 벡터의 내적과 행렬의 곱
1.1.5 행렬 형상 확인
1.2 신경망의 추론
1.2.1 신경망 추론 전체 그림
신경망 : 함수처럼 입력을 출력으로 변환
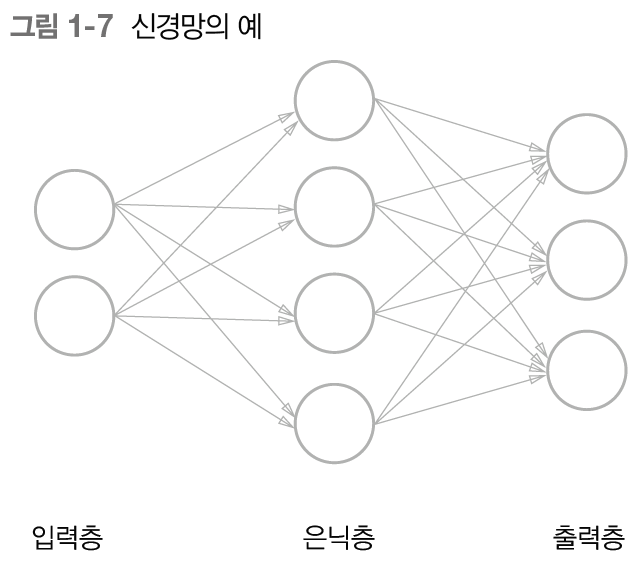


- 은닉층의 뉴런은 가중치의 합으로 계산
- 행렬의 곱으로 한번에 계산할 수 있음
- 완전연결 계층이 수행하는 변환은 행렬의 곱을 이용해 위와 같이 정리
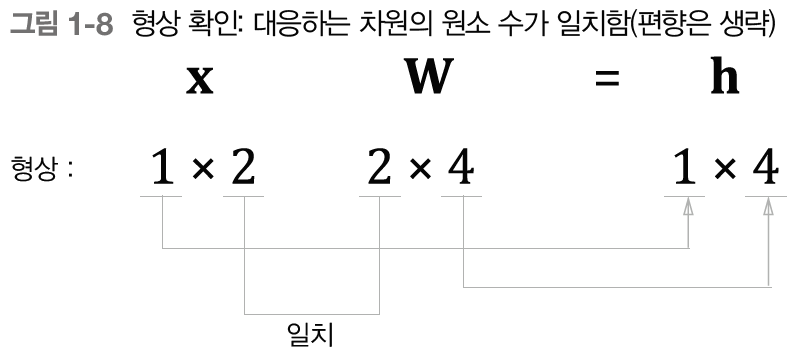


- 완전연결계층에 의한 변환은 '선형' 변환
- 비선형 활성화 함수를 이용함으로써 신경망의 표현력을 높임
→ 시그모이드 함수 (S자 모양의 곡선 함수)

시그모이드 함수
- 비선형 변환을 가능하게 함
- 실수를 입력받아 0~1 사이의 실수 출력
1.2.2 계층으로 클래스화 및 순전파 구현
- 순전파 : 추론 과정에서 하는 처리
- 역전파 : 학습 과정에서 데이터(기울기)를 순전파와 반대 방향으로 전파
모듈화 해두면 블록을 조합하듯 신경망을 구축할 수 있음
1.3 신경망의 학습
신경망의 학습 = 최적의 매개변수 값을 찾는 작업
1.3.1 손실 함수
신경망 학습에는 학습이 얼마나 잘 되고 있는지 알기 위한 '척도' 필요
손실
- 학습 단계의 특정 시점에서 신경망의 성능을 나타내는 척도
- 학습 데이터(정답)와 신경망이 예측한 결과를 비교하여 예측이 얼마나 나쁜가를 산출한 단일 값(스칼라)
- 손실 함수(loss function)을 사용하여 구함
- 다중 클래스 분류 신경망에서는 주로 '교차 엔트로피 오차(Cross Entropy Error)'를 손실 함수로 이용
교차 엔트로피 오차(Cross Entropy Error)
- 신경망이 출력하는 각 클래스의 '확률'과 '정답 레이블'을 구할 수 있음

신경망 구성 예시
- x : 입력 데이터, t : 정답 레이블, L : 손실
- Sigmoid 함수를 통해 비선형 변환 가능
- Softmax 계층의 출력은 확률이 되어, 다음 계층인 Cross Entropy Error 계층에는 확률과 정답 레이블 입력
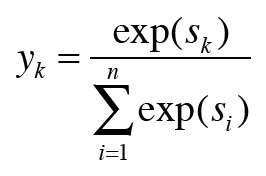
- 출력이 총 n개일 때, k번째 출력 yk를 구하는 계산식
- yk는 k번째 클래스에 해당하는 소프트맥스 함수의 출력
- 출력의 각 원소는 0.0 ~ 1.0 사이의 실수, 각 원소 모두 더하면 1.0 → 출력을 '확률'로 해석
- 출력 '확률'이 교차 엔트로피 오차의 입력으로 들어감
* exp(s) : e**s


- tnk는 n번째 데이터의 k차원째 값
- ynk는 신경망의 출력, tnk는 정답 레이블 ( 정답은 원핫 벡터로 표기 ex.[0, 1, 0, 0, 0] )
- [식 1.8]에서는 N으로 나눠서 1개당 '평균 손실 함수'를 구함 → 미니배치 크기에 관계없이 항상 일관된 척도
책에서는 '소프트맥스 함수'와 '교차 엔트로피 오차'를 계산하는 계층을 Softmax with Loss 계층 하나로 구현
→ 두 계층을 통합하면 역전파 계산이 쉬워지기 때문

1.3.2 미분과 기울기
신경망 학습의 목표는 손실을 최소화하는 매개변수를 찾는 것



- 중요 : W(행렬)과 ∂L / ∂W 의 형상이 같다는 점
1.3.3 연쇄 법칙
- 신경망의 기울기 구하는 법 = 오차역전파
- 오차역전파 이해하는 법 = 연쇄 법칙

아무리 많은 함수를 연결하더라도, 그 미분은 개별 함수의 미분들을 이용해 구할 수 있음
1.3.4 계산 그래프
계산 그래프 : 계산 과정을 시각적으로 보여줌



- 목표 : L의 미분(기울기)을 각 변수에 대해 구하는 것
- 역전파에서 '전파되는 값' = 최종 출력 L의 각 변수에 대한 미분
- 연쇄 법칙에 따르면 역전파로 흐르는 미분 값은 상류로부터 흘러온 미분과 각 연산 노드의 국소적인 미분을 곱해 계산할 수 있음
ex) ∂L / ∂x = ∂L / ∂x * ∂z / ∂x & ∂L/ ∂y = ∂L / ∂z * ∂z / ∂y
곱셈 노드 역전파
- '상류로부터 받은 기울기'에 '순전파 시의 입력을 서로 바꾼 값'을 곱함

분기 노드 역전파
- 상류에서 온 기울기들의 '합'

Repeat 노드 역전파
- 2개로 분기하는 분기 노드를 일반화하면 N개로의 분기(복제)
- N개의 기울기를 모두 더해 구함

Sum 노드 역전파
- 범용 덧셈 노드
- 상류로부터의 기울기를 모든 화살표에 분배
- Repeat 노드와 서로 '반대 관계'

MatMul 노드 역전파 (Matrix Multiply)
- '순전파 시의 입력을 서로 바꾼 행렬' 사용 (곱셈의 역전파와 비슷)

1.3.5 기울기 도출과 역전파 구현
Sigmoid 계층 역전파
- 출력 쪽 계층으로부터 전해진 기울기에, 시그모이드 함수의 미분을 곱, 입력 쪽 계층으로 전파


Affine 계층
- Affine 계층의 순전파 y = np.matmul(x, W) + b

Softmax with Loss 계층
- 소프트맥스 함수와 교차 엔트로피 오차를 하나의 계층으로 구현
- 역전파가 깔끔하게 떨어짐, 자신의 출력과 정답 레이블의 차이
- 신경망의 역전파는 이 차이(오차)를 앞 계층에 전해주는 것으로, 신경망 학습에서 아주 중요한 성질

1.3.6 가중치 갱신
신경망의 학습 순서
- 1단계 : 미니배치
- 훈련 데이터 중에서 무작위로 다수의 데이터를 골라낸다. - 2단계 : 기울기 계산
- 오차역전파법으로 각 가중치 매개변수에 대한 손실 함수의 기울기를 구한다. - 3단계 : 매개변수 갱신
- 기울기를 사용하여 가중치 매개변수를 갱신한다. - 4단계 : 반복
- 1~3단계를 필요한 만큼 반복한다.
* 3단계의 가중치 갱신 기법 종류는 아주 다양함
- 그 중 하나는 SGD 방식
경사하강법(Gradient Descent)
- 오차역전파법으로 가중치의 기울기를 얻음
- 기울기는 현재 가중치 매개변수에서 손실을 가장 크게 하는 방향
- 매개변수를 그 기울기와 반대방향으로 갱신하면 손실을 줄일 수 있음
확률적경사하강법(SGD)
- 확률적 = 무작위로 선택된 데이터(미니배치)에 대한 기울기 이용
- (현재의) 가중치를 기울기 방향으로 일정한 거리만큼 갱신
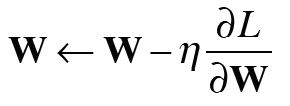
1.4 신경망으로 문제를 풀다
1.4.1 스파이럴 데이터셋
1.4.2 신경망 구현
1.4.3 학습용 코드
1.4.4 Trainer 클래스
1.5 계산 고속화
1.5.1 비트 정밀도
1.5.2 GPU(쿠파이)
1.6 정리
- 신경망은 입력층, 은닉층(중간층), 출력층을 지닌다.
- 완전연결계층에 의해 선형 변환이 이뤄지고, 활성화 함수에 의해 비선형 변환이 이뤄진다.
- 완전연결계층이나 미니배치 처리는 행렬로 모아 한꺼번에 계산할 수 있다.
- 오차역전파법을 사용하여 신경망의 손실에 관한 기울기를 효율적으로 구할 수 있다.
- 신경망이 수행하는 처리는 계산 그래프로 시각화할 수 있으며, 순전파와 역전파를 이해하는 데 도움이 된다.
- 신경망의 구성요소들을 '계층'으로 모듈화해두면, 이를 조립하여 신경망을 쉽게 구성할 수 있다.
- 신경망 고속화에는 GPU를 이용한 병렬 계산과 데이터의 비트 정밀도가 중요하다.