[전편]
37. 텐서를 다루다
38. 형상 변환 함수
39. 합계 함수
40. 브로드캐스트 함수
41. 행렬의 곱
42. 선형 회귀
43. 신경망
-------------------------------------------------------
[후편]
44. 매개변수를 모아두는 계층
45. 계층을 모아두는 계층
46. Optimizer로 수행하는 매개변수 갱신
47. 소프트맥스 함수와 교차 엔트로피 오차
48. 다중 클래스 분류
49. Dataset 클래스와 전처리
50. 미니배치를 뽑아주는 DataLoader
51. MNIST 학습
칼럼
44. 매개변수를 모아두는 계층
'사용 편의성' 면에서 몇 가지 문제
매개변수 담는 구조를 만들자
→ Parameter & Layer 클래스
이 두 클래스로 매개변수 관리를 자동화할 수 있음
44.1 Parameter 클래스 구현
Parameter 클래스 : Variable 클래스와 똑같은 기능
class Parameter(Variable):
pass- Variable 클래스를 상속, 기능도 동일
- Parameter 인스턴스와 Variable 인스턴스는 기능은 같지만 구별할 수 있음
ex) 두 인스턴스를 만들고 isinstance(p.Parameter)를 사용하면 True, False로 구분됨 - Parameter 인스턴스와 Variable 인스턴스를 조합하여 계산할 수 있음, isinstance 함수로 구분
- 이 점을 이용하여 Parameter 인스턴스만을 담는 구조 만듦
* NOTE
- Parameter 클래스는 dezero/core.py에 추가
- dezero/__init__.py에 from dezero.core import Parameter라는 한 줄 추가
- 그러면 DeZero를 사용하는 사람은 from dezero import Parameter로 임포트할 수 있음
44.2 Layer 클래스 구현
Layer 클래스
- 공통점 : Function 클래스와 마찬가지로 변수를 변환하는 클래스
- 차이점 : 매개변수를 유지한다는 점
- Layer 클래스는 매개변수를 유지하고 매개변수를 사용하여 변환하는 클래스
* NOTE
Layer 클래스를 기반 클래스로 두고 구체적인 변환은 자식 클래스에서 구현
Layer 클래스의 구현
class Layer:
def __init__(self):
self._params = set()
def __setattr__(self, name, value):
if isinstance(value, (Parameter, Layer)):
self._params.add(name)
super().__setattr__(name, value)- _params라는 인스턴스 변수 : Layer 인스턴스에 속한 매개변수를 보관
- 위에서 value가 Parameter 인스턴스라면 self._params에 name을 추가
→ Layer 클래스가 갖는 매개변수를 인스턴스 변수 _params에 모아둘 수 있음 - 이와 같이 layer 인스턴스 변수를 설정하면, Parameter 인스턴스를 보유하고 있는 인스턴스 이름만 layer._params에 추가
- 인스턴스 변수 __dict__에는 모든 인스턴스 변수가 딕셔너리 타입으로 저장되므로, Parameter 인스턴스만 꺼낼 수 있음
* CAUTION
- 인스턴스 변수 _params의 타입은 '집합(set)'
- 리스트와 달리 원소들에 순서가 없고, ID가 같은 객체는 중복 저장할 수 없음
__setattr__(self, name, value)
- 인스턴스 변수를 설정할 때 호출되는 특수 메서드
- 이름이 name인 인스턴스 변수에 값을 value로 전달
- 메서드를 재정의(override)하면 인스턴스 변수를 설정할 때 로직 추가할 수 있음
Layer 클래스에 다음 4개의 메서드를 추가
class Layer:
...
def __call__(self, *inputs):
outputs = self.forward(*inputs)
if not isinstance(outputs, tuple):
outputs = (outputs,)
self.inputs = [weakref.ref(x) for x in inputs]
self.outputs = [weakref.ref(y) for y in outputs]
return outputs if len(outputs) > 1 else outputs[0]
def forward(self, inputs):
raise NotImplementedError()
def params(self):
for name in self._params:
obj = self.__dict__[name]
if isinstance(obj, Layer):
yield from obj.params()
else:
yield obj
def cleargrads(self):
for param in self.params():
param.cleargrad()
__call__ 메서드
- 입력받은 인수를 건네 forward 메서드 호출
- 출력이 하나뿐이라면 튜플이 아닌, 그 출력 직접 반환
- 나중을 생각하여 입력과 출력 변수를 약한 참조로 유지
forward 메서드
- 자식 클래스에서 구현할 것
params 메서드
- Layer 인스턴스에 담겨 있는 Parameter 인스턴스 꺼내줌
cleargrads 메서드
- 모든 매개변수의 기울기를 재설정
- 복수형 s : Layer가 가진 '모든' 매개변수에 대해 (단수형) cleargras를 호출
* NOTE
- params 메서드는 yeild를 사용하여 값 반환
- yield는 return처럼 사용
- return은 처리 종료하고 값 반환, yield는 처리를 '일시 중지'하고 반환
- yield 사용하면 작업 재개할 수 있음
→ 앞의 에에서 params 메서드 호출시 일시 중지 됐던 처리 재개, 매개변수 순차적으로 꺼냄
44.3 Linear 클래스 구현
선형 변환 수행
class Linear(Layer):
def __init__(self, out_size, nobias=False, dtype=np.float32, in_size=None):
super().__init__()
self.in_size = in_size
self.out_size = out_size
self.dtype = dtype
self.W = Parameter(None, name='W')
if self.in_size is not None:
self._init_W()
if nobias:
self.b = None
else:
self.b = Parameter(np.zeros(out_size, dtype=dtype), name='b')
def _init_W(self, xp=np):
I, O = self.in_size, self.out_size
W_data = xp.random.randn(I, O).astype(self.dtype) * np.sqrt(1 / I)
self.W.data = W_data
def forward(self, x):
if self.W.data is None:
self.in_size = x.shape[1]
xp = cuda.get_array_module(x)
self._init_W(xp)
y = F.linear(x, self.W, self.b)
return y- Linear 클래스는 Layer 클래스 상속하여 구현
- __init__(self, in_size, out_size, nobias) : 입력 크기, 출력 크기, 편향 사용 여부 플래그
- 위 코드에서는 in_size를 지정하지 않아도 됨
- forward(self, x) 메서드에서 입력 x의 크기에 맞게 가중치 데이터를 생성 => 사용성 좋아짐 - 가중치와 편향은 self.W, self.b 형태로 Parameter 인스턴스를 인스턴스 변수에 설정
(위 코드는 가중치 W 생성 시점 늦추는 방식)
→ 두 Parameter 인스턴스 변수의 이름이 self._params에 추가 - forward 메서드로 선형 변환 구현
* NOTE
- LInear 클래스의 가중치 초깃값은 무작위로 설정해야 함
44.4 Layer를 이용한 신경망 구현
sin 함수의 데이터셋에 대한 회귀 문제 다시!
if '__file__' in globals():
import os, sys
sys.path.append(os.path.join(os.path.dirname(__file__), '..'))
import numpy as np
import dezero.functions as F
import dezero.layers as L *
np.random.seed(0)
x = np.random.rand(100, 1)
y = np.sin(2 * np.pi * x) + np.random.rand(100, 1)
l1 = L.Linear(10) *
l2 = L.Linear(1) *
def predict(x):
y = l1(x) *
y = F.sigmoid(y)
y = l2(y) *
return y
lr = 0.2
iters = 10000
for i in range(iters):
y_pred = predict(x)
loss = F.mean_squared_error(y, y_pred)
l1.cleargrads() *
l2.cleargrads() *
loss.backward()
for l in [l1, l2]: *
for p in l.params(): *
p.data -= lr * p.grad.data *
if i % 1000 == 0:
print(loss)- 매개변수 관리를 Linear 인스턴스가 맡고 있음
- 매개변수 기울기 재설정과 매개변수 갱신 작업이 전보다 깔끔
- Linear 클래스를 개별적으로 다루는 부분을 다음 단계에서 개선!
여러 Layer를 하나의 클래스로 묶어서 관리
45. 계층을 모아두는 계층
Layer 인스턴스 자체도 관리가 필요하므로 확장!
45.1 Layer 클래스 확장
- 현재 : 여러 개 Parameter 가질 수 있음
- 확장 : Layer 클래스가 '다른 Layer'도 담을 수 있게 확장
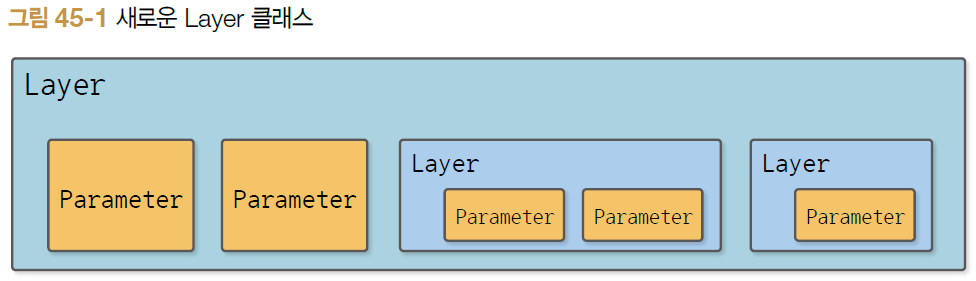
- '상자' 구조
- 목표 : 바깥 layer에서 그 안에 존재하는 모든 매개변수를 꺼낼 수 있도록
class Layer:
def __init__(self):
self._params = set()
def __setattr__(self, name, value):
if isinstance(value, (Parameter, Layer)): # 1. Layer도 추가
self._params.add(name)
super().__setattr__(name, value)
def params(self):
for name in self._params:
obj = self.__dict__[name]
if isinstance(obj, Layer): # 2. Layer에서 매개변수 꺼내기
yield from obj.params()
else:
yield obj1. 인스턴스 변수를 설정할 때 Layer 인스턴스의 이름도 _params에 추가
2. 매개변수를 꺼내는 처리
- params 메서드는 _params에서 name(문자열)을 꺼내 그 name에 해당하는 객체를 obj로 꺼냄
- obj가 Layer 인스턴스라면 obj.params()를 호출
- Layer 속 Layer에서도 매개변수를 재귀적으로 꺼낼 수 있음
* CAUTION : 제너레이터(generator)
- yield를 사용한 함수
- 제너레이터를 사용하여 또 다른 제너레이터를 만들고자 할 때는 yield from 사용
새로운 Layer 클래스
import dezero.layers as L
import dezero.functions as F
from dezero import Layer
model = Layer()
model.l1 = L.Linear(5) # 출력 크기만 지정
model.l2 = L.Linear(3)
# 추론을 수행하는 함수
def predict(model, x):
y = model.l1(x)
y = F.sigmoid(y)
y.model.l2(y)
return y
# 모든 매개변수에 접근
for p in model.params():
print(p)
# 모든 매개변수의 기울기를 재설정
model.cleargrads()- model=Layer()에서 인스턴스 생성
- model의 인스턴스 변수로 Linear 인스턴스를 추가
- 추론을 수행하는 predict(model.x) 구현
- (중요) model.params( )로 model 내에 존재하는 모든 매개변수에 접근
- model.cleargrads( )는 모든 매개변수의 기울기를 재설정
- Layer 클래스를 이용하여 신경망에서 사용하는 매개변수를 한꺼번에 관리
Layer 클래스를 더 편리하게 사용하는 방법
= Layer 클래스를 상속하여 모델 전체를 하나의 '클래스'로 정의하는 방법
# Model definition
class TwoLayerNet(Model):
def __init__(self, hidden_size, out_size):
super().__init__()
self.l1 = L.Linear(hidden_size)
self.l2 = L.Linear(out_size)
def forward(self, x):
y = F.sigmoid(self.l1(x))
y = self.l2(y)
return y- TwoLayerNet이라는 이름으로 클래스 모델을 정의
- 이 클래스는 Layer 상속
- __init__와 forward 메서드 구현
- __init__ 메서드 : 필요한 Layer들을 생성
- forward 메서드 : 추론을 수행하는 코드 작성
- 이처럼 하나의 클래스에 신경망에 필요한 모든 코드 집약할 수 있음
* NOTE
객체지향식 모델 정의 방법(모델을 클래스 단위로 정의)은 체이너가 최초로 제안
45.3 Model 클래스
모델
- 사물의 본질을 단순하게 표현한 것'
- 복잡한 패턴이나 규칙이 숨어 있는 현상을 수식을 사용하여 단순하게 표현
- 신경망도 수식으로 표현할 수 있는 함수 = 모델
Model 클래스
- 모델을 표현하기 위함
- Layer 클래스의 기능을 이어받고, 시각화 메서드가 하나 추가
class Model(Layer):
def plot(self, *inputs, to_file='model.png'):
y = self.forward(*inputs)
return utils.plot_dot_graph(y, verbose=True, to_file=to_file)- Model은 Layer를 상속
- Layer 클래스처럼 활용할 수도 있음
- 시각화를 위한 plot 메서드가 추가
: *inputs로 전달받은 데이터를 forward 메서드로 계산한 다음, 생성된 계산 그래프를 이미지 파일로 내보냄
사용 코드
import numpy as np
from dezero import Variable, Model
import dezer.layers as L
import dezero.functions as F
class TwoLayerNet(Model):
def __init__(self, hidden_size, out_size):
super().__init__()
self.l1 = L.Linear(hidden_size)
self.l2 = L.Linear(out_size)
delf forward(self, x):
y = F.sigmoid(self.l1(x))
y = self.l2(y)
return y
x = Variable(np.random.randn(5, 10), name='x')
model = TwoLayerNet(100, 10)
model.plot(x)
- Model 클래스는 Layer 클래스처럼 활용할 수 있음
- 계산 그래프를 시각화해주는 메서드도 제공
45.3 Model을 사용한 문제 해결
sin 함수로 생성한 데이터셋 회귀 문제를 Model 클래스를 이용하여 다시 풀어보자
if '__file__' in globals():
import os, sys
sys.path.append(os.path.join(os.path.dirname(__file__), '..'))
import numpy as np
from dezero import Model
import dezero.layers as L
import dezero.functions as F
# 데이터셋 생성
np.random.seed(0)
x = np.random.rand(100, 1)
y = np.sin(2 * np.pi * x) + np.random.rand(100, 1)
# 하이퍼파라미터 설정
lr = 0.2
max_iter = 10000
hidden_size = 10
# 모델 정의
class TwoLayerNet(Model):
def __init__(self, hidden_size, out_size):
super().__init__()
self.l1 = L.Linear(hidden_size)
self.l2 = L.Linear(out_size)
def forward(self, x):
y = F.sigmoid(self.l1(x))
y = self.l2(y)
return y
model = TwoLayerNet(hidden_size, 1)
# 학습 시작
for i in range(max_iter):
y_pred = model(x)
loss = F.mean_squared_error(y, y_pred)
model.cleargrads()
loss.backward()
for p in model.params():
p.data -= lr * p.grad.data
if i % 1000 == 0:
print(loss)- Model 클래스를 상속한 TwoLayerNet으로 신경망 구성
- 덕분에 for문 안의 코드가 더 간단
- 모든 매개변수는 model을 통해 접근
- 매개변수의 기울기 재설정 model.cleargrads()로 처리
이제 모든 매개변수 관리를 Model 클래스(또는 Layer 클래스)로 할 수 있음
45.4 MLP 클래스
이전 층이 2개인 완전연결계층 모델을 구현했음
class TwoLayerNet(Model):
def __init__(self, hidden_size, out_size):
super().__init__()
self.l1 = L.Linear(hidden_size)
self.l2 = L.Linear(out_size)
def forward(self, x):
y = F.sigmoid(self.l1(x))
y = self.l2(y)
return y
앞으로를 위해 더 범용적인 완전연결계층 신경망 구현
import dezero.functions as F
import dezero.layers as L
class MLP(Model):
def __init__(self, fc_output_sizes, activation=F.sigmoid):
super().__init__()
self.activation = activation
self.layers = []
for i, out_size in enumerate(fc_output_sizes):
layer = L.Linear(out_size)
setattr(self, 'l' + str(i), layer)
self.layers.append(layer)
def forward(self, x):
for l in self.layers[:-1]:
x = self.activation(l(x))
return self.layers[-1](x)초기화
- fc_output_sizes : fc는 full connect(완전연결)의 약자, 신경망을 구성하는 완전연결계층들의 출력 크기를 튜플 또는 리스트로 저장
- ex) (10, 10, 1)은 첫번째 계층 출력 크기 10, 두 번째 계층 10, 마지막 계층 1 ...
주의
- 인스턴스 변수 설정을 setattr 함수로 하고 있음
- DeZero는 계층 모델에 인스턴스 변수를 설정하는 식으로 계층에 포함된 매개변수들을 관리
* NOTE : MLP
- Multi-Layer perceptron의 약자 '다층 퍼셉트론'
46. Optimizer로 수행하는 매개변수 갱신
딥러닝에서 경사하강법 외에도 다양한 최적화 기법 제안
매개변수 갱신 작업(갱신 코드)을 모듈화하고 쉽게 다른 모듈로 대체할 수 있는 구조 만들자
46.1 Optimizer 클래스
- 매개변수 갱신을 위한 기반 클래스
- Optimizer가 기초를 제공
- 구체적인 최적화 기법은 Optimizer 클래스를 상속한 곳에서 구현
class Optimizer:
def __init__(self):
self.target = None
self.hooks = []
def setup(self, target):
self.target = target
return self
def update(self):
params = [p for p in self.target.params() if p.grad is not None]
for f in self.hooks:
f(params)
for param in params:
self.update_one(param)
def update_one(self, param):
raise NotImplementedError()
def add_hook(self, f):
self.hooks.append(f)초기화 메서드
- target과 hooks라는 두 개의 인스턴스 변수 초기화
setup 메서드
- 매개변수를 갖는 클래스(Model 또는 Layer)를 인스턴스 변수인 target으로 설정
Optimizer 클래스
- 매개변수 갱신에 앞서 전체 매개변수 전처리 기능도 갖춤
- 원하는 전처리가 있다면 add_hook 메서드를 사용하여 전처리를 수행하는 함수를 추가
→ 가중치 감소, 기울리 클리핑 같은 기법 이용 가능
46.2 SGD 클래스 구현
경사하강법으로 매개변수를 갱신하는 클래스
class SGD(Optimizer):
def __init__(self, lr=0.01):
super().__init__()
self.lr = lr
def update_one(self, param):
param.data -= self.lr * param.grad.data- Optimizer 클래스를 상속
- __init__ 메서드는 학습률을 받아 초기화
- update_one 메서드에서 매개변수 갱신 코드를 구현
매개변수 갱신을 SGD 클래스에게 맡기자
* NOTE : SGD
확률적경사하강법(Stochastic Gradient Descent)의 약자
'확률적'은 대상 데이터 중에서 무작위로(확률적으로) 선별한 데이터에 대해 경사하강법을 수행
딥러닝에서는 원래 데이터에서 무작위로 골라 경사하강법을 수행하는 것이 일반적
46.3 SGD 클래스를 사용한 문제 해결
SDG 클래스로 이전 단계와 같은 문제 해결해보자
if '__file__' in globals():
import os, sys
sys.path.append(os.path.join(os.path.dirname(__file__), '..'))
import numpy as np
from dezero import optimizers *
import dezero.functions as F
from dezero.models import MLP
np.random.seed(0)
x = np.random.rand(100, 1)
y = np.sin(2 * np.pi * x) + np.random.rand(100, 1)
lr = 0.2
max_iter = 10000
hidden_size = 10
model = MLP((hidden_size, 1)) *
optimizer = optimizers.SGD(lr).setup(model) *
for i in range(max_iter):
y_pred = model(x)
loss = F.mean_squared_error(y, y_pred)
model.cleargrads()
loss.backward()
optimizer.update() *
if i % 1000 == 0:
print(loss)- SGD 클래스로 매개변수 갱신
46.4 SGD 이외의 최적화 기법
기울기를 이용한 최적화 기법 다양함
ex) Momentum, AdaGrad, AdaDelta, Adam ...
Optimizer 클래스 도입의 목표
- 다양한 최적화 기법을 필요에 따라 손쉽게 전환하기 위해
- Optimizer를 상속하여 다양한 최적화 기법을 구현하자
Momentum 구현


- W : 갱신할 가중치 매개변수
- ∂ 부분 : 기울기
- ∏ : 학습률
- v : 물리에서 말하는 '속도'
- av : 물체가 아무런 힘을 받지 않을 때 서서히 감속시키는 역할 (a 값으로 0.9 등을 설정)
[식 46.1] : 물체가 기울기 방향으로 힘을 받아 가속된다는 물리 법칙 나타냄
[식 46.2] : 속도만큼 위치(매개변수)가 이동
class MomentumSGD(Optimizer):
def __init__(self, lr=0.01, momentum=0.9):
super().__init__()
self.lr = lr
self.momentum = momentum
self.vs = {}
def update_one(self, param):
v_key = id(param)
if v_key not in self.vs:
xp = cuda.get_array_module(param.data)
self.vs[v_key] = xp.zeros_like(param.data)
v = self.vs[v_key]
v *= self.momentum
v -= self.lr * param.grad.data
param.data += v- 각 매개변수에는 '속도'에 해당하는 데이터 있음
- 딕셔너리 타입의 인스턴스 변수 self.vs에 유지
손쉽게 Momentum으로 전환 가능
optimizer = SGD(lr)을 optimizer = MomentumSGD(lr)로 바꿔주면 됨
47. 소프트맥스 함수와 교차 엔트로피 오차
다중 클래스 분류(multi-class classification)
47.1 슬라이스 조작 함수
get_item (편의 함수)
- Variable의 다차원 배열 중에서 일부를 슬라이스하여 뽑아줌
- (2, 3) 형상의 x에서 1번째 행의 원소 추출
x = Variable(np.array([[1, 2, 3], [4, 5, 6]]))
y = F.get_item(x, 1)
print(y)
# 출력 결과
variable([4 5 6])
y.backward()
print(x.grad)
# 실행 결과
variable([0. 0. 0.]
[1. 1. 1.]])- y.backward()를 호출하여 역전파
- 슬라이스로 인한 '계산'은 다차원 배열의 데이터 일부를 수정하지 않고 전달하는 것
- 역전파는 원래 다차원 배열에서 데이터가 추출된 위치에 해당 기울기를 설정하고, 그 외에는 0으로 설정

* NOTE : 슬라이스
- 다차원 배열의 일부를 추출하는 작업
get_item 함수로 인덱스 반복 지정 → 동일한 원소 여러 번 빼냄
x = Variable(np.array([[1, 2, 3], [4, 5, 6]]))
indices = np.array([0, 0, 1])
y = F.get_item(x, indices)
print(y)
# 실행결과
variable([1 2 3]
[1 2 3]
[4 5 6]])
get_item 함수를 Variable의 메서드로도 사용할 수 있도록 특수 메서드로 설정
Variable.__getitem__ = F.get_item # Variable의 메서드로 설정
y = x[1]
print(y)
y = x[:,2]
print(y)
# 실행결과
variable([4 5 6])
variable([3 6])- 슬라이스 작업의 역전파도 올바르게 이루어짐
47.2 소프트맥스 함수
다중 클래스 분류를 신경망으로 → 선형 회귀 신경망 그대로 사용
ex) 입력 데이터의 차원 수가 2이고 3개의 클래스로 분류하는 문제
from dezero.models import MLP
model = MLP((10, 3))- MLP((10, 3)) : 2층으로 된 완전연결 신경망 만들어줌 (출력 크기 각각 10, 3)
- model은 입력 데이터를 3차원 벡터(원소가 3개인 벡터)로 변환
실행 코드
x = np.array([0.2, -0.4]])
y = model(x)
print(y)
# 실행결과
variable([[-0.61 -0.42 0.31]])- x의 형상 (1, 2) : 샘플 데이터가 1개, 그 데이터는 원소가 2개인 2차원 벡터
- 신경망 출력 형태 (1, 3) : 샘플 데이터가 3개의 원소(3차원 벡터)로 변환됨
- 3차원 벡터의 원소 각각이 하나의 클래스에 해당 → 가장 큰 원소의 인덱스가 이 모델이 분류한 정답 클래스
(여기에서는 2번 원소)
* NOTE
- 여러 데이터를 한꺼번에 처리할 수 있음
- ex) x = np.array([[0.2, -0.4], [0.3, 0.5], [1.3, -3.2], [2.1, 0.3]]) → 4개의 입력 데이터 하나로 묶어 전달
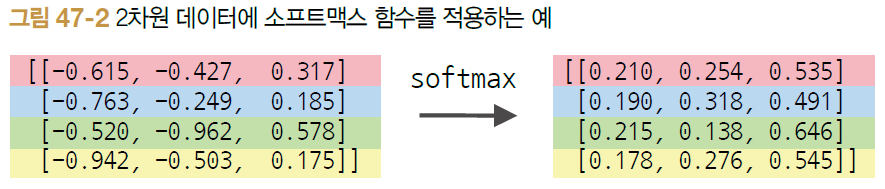
신경망 출력의 단순한 '수치'를 '확률'로 변환 ==> 소프트맥스 함수

- 소프트맥스 함수의 입력 y_k개 총 n개라고 가정(n은 클래스 수)
- [식 47.1]은 k번째 출력 p_k를 구하는 계산식
- 소프트맥스 함수의 분자는 입력 y_k의 지수 함수, 분모는 모든 입력의 지수 함수의 총합
- 0 <= p_i <= 1, 모든 p의 합은 1이 성립 → (p1, p2, ..., p_n) 원소 각각을 확률로 해석할 수 있게 됨
DeZero용 소프트맥스 함수 구현 (입력 데이터가 하나인 경우에 한정)
if '__file__' in globals():
import os, sys
sys.path.append(os.path.join(os.path.dirname(__file__), '..'))
import numpy as np
np.random.seed(0)
from dezero import Variable, as_variable
import dezero.functions as F
from dezero.models import MLP
def softmax1d(x):
x = as_variable(x)
y = F.exp(x)
sum_y = F.sum(y)
return y / sum_y
model = MLP((10, 3))
x = Variable(np.array([[0.2, -0.4]]))
y = model(x)
p = softmax1d(y)
print(y)
print(p)
x = np.array([[0.2, -0.4], [0.3, 0.5], [1.3, -3.2], [2.1, 0.3]])
t = np.array([2, 0, 1, 0])
y = model(x)
p = F.softmax_simple(y)
print(y)
print(p)
loss = F.softmax_cross_entropy_simple(y, t)
loss.backward()
print(loss)- 결과로 출력된 p의 각 원소는 0 이상 1 이하이고, 총합은 1
- 신경망의 출력을 '확률'로 변환할 수 있음
* CAUTION
- 소프트맥스 함수의 계산은 지수 함수로 이루어짐 → 결괏값이 너무 커지거나 작아지기 쉬움
- 오버플로 문제에 잘 대해줘야 함
DeZero용 소프트맥스 함수 구현 (배치 데이터에도 적용할 수 있는 형태)
def softmax_simple(x, axis=1):
x = as_variable(x)
y = exp(x)
sum_y = sum(y, axis=axis, keepdims=True)
return y / sum_y- 인수 x는 2차원 데이터라고 가정
- 인수 axis에서 어떤 축을 따라 소프트맥스 함수를 적용할지 정함
- 더 나은 구현 방식은 Function 클래스를 상속하여 sortmax 클래스를 구현하고 파이썬 함수로 softmax를 구현하는 것
47.3 교차 엔트로피 오차
다중 클래스 분류에 적합한 손실 함수

- t_k는 정답 데이터의 k차원째 값
- 정답 데이터의 각 원소는 정답에 해당하는 클래스면 1로, 그렇지 않으면 0으로 (원핫 벡터)
- p_k는 신경망에서 소프트맥스 함수를 적용한 후의 출력
더 간단한 표현

- p[t]는 벡터 p에서 t번째 요소만을 추출한다는 뜻
* CAUTION
- 이번 교차 엔트로피 오차 설명은 데이터가 하나인 경우에 대한 것
- 데이터가 N개라면 각 데이터에서 교차 엔트로피 오차를 구하고, 전체를 더한 다음 N으로 나눔
= 평균 교차 엔트로피 오차 구함
'소프트맥스 함수'와 '교차 엔트로피 오차'를 한꺼번에 수행하는 함수
def softmax_cross_entropy_simple(x, t):
x, t = as_variable(x), as_variable(t)
N = x.shape[0]
p = softmax(x)
p = clip(p, 1e-15, 1.0) # To avoid log(0)
log_p = log(p)
tlog_p = log_p[np.arange(N), t.data]
y = -1 * sum(tlog_p) / N
return y- x : 신경망에서 소프트맥스 함수를 적용하기 전의 출력
- t : 정답 데이터 (정답 클래스 번호가 주어진다고 가정)
- p = softmax(x)에서 p의 원솟값은 0 이상 1 이하
- log는 0을 건네면 오류가 생기므로, 아주 작은 값으로 대체(clip함수)
* clip(x, x_min, x_max)
- x_min 이하이면 x_min으로 변환, x_max 이상이면 x_max로 변환
* np.arange(N)
- [0, 1, ..., N-1] 형태의 ndarray 인스턴스 생성
* log_p[np.arange(N), t.data]
- log_p[0, t.data[0]], log_p[1, t.data[1]], ...와 정답 데이터(t.data)에 대응하는 모델의 출력 구함
다중 클래스 분류를 하는 신경망에 구체적인 데이터를 주어 교차 엔트로피 오차 계산
x = np.array[[0.2, -0.4], [0.3, 0.5], [1.3, -3.2], [2.1, 0.3]])
t = np.array([2, 0, 1, 0])
y = model(x)
loss = F.softmax_cross_entropy_simple(y, t)
print(loss- 입력 데이터 x와 정답 데이터 t를 준비
- y = model(x)에서 변환
- F.softmax_cross_entropy_simple(y, t)에서 손실 함수 계산
48. 다중 클래스 분류
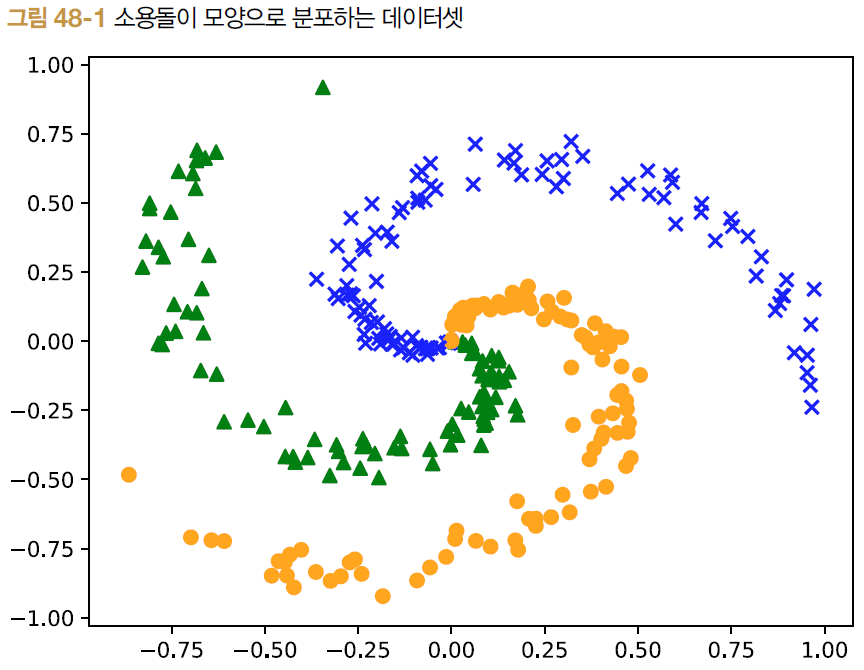
48.1 스파이럴 데이터셋
get_spiral 함수 사용
- train 플래그 : True면 학습(훈련)용 데이터 반환, False 면 테스트용 데이터 반환
- 3 클래스 분류 (t의 원소 0, 1, 2)
48.2 학습 코드
다중 클래스 분류하는 코드
if '__file__' in globals():
import os, sys
sys.path.append(os.path.join(os.path.dirname(__file__), '..'))
import math
import numpy as np
import matplotlib.pyplot as plt
import dezero
from dezero import optimizers
import dezero.functions as F
from dezero.models import MLP
# 1. 하이퍼파라미터 설정
max_epoch = 300
batch_size = 30
hidden_size = 10
lr = 1.0
# 2. 데이터 읽기 / 모델, 옵티마이저 생성
x, t = dezero.datasets.get_spiral(train=True)
model = MLP((hidden_size, 3))
optimizer = optimizers.SGD(lr).setup(model)
data_size = len(x)
max_iter = math.ceil(data_size / batch_size)
for epoch in range(max_epoch):
# 3. 데이터셋의 인덱스 뒤섞기
index = np.random.permutation(data_size)
sum_loss = 0
for i in range(max_iter):
# 4. 미니배치 생성
batch_index = index[i * batch_size:(i + 1) * batch_size]
batch_x = x[batch_index]
batch_t = t[batch_index]
# 5. 기울기 산출 / 매개변수 갱신
y = model(batch_x)
loss = F.softmax_cross_entropy(y, batch_t)
model.cleargrads()
loss.backward()
optimizer.update()
sum_loss += float(loss.data) * len(batch_t)
# 6. 에포크마다 학습 경과 출력
avg_loss = sum_loss / data_size
print('epoch %d, loss %.2f' % (epoch + 1, avg_loss))
# Plot boundary area the model predict
h = 0.001
x_min, x_max = x[:, 0].min() - .1, x[:, 0].max() + .1
y_min, y_max = x[:, 1].min() - .1, x[:, 1].max() + .1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
X = np.c_[xx.ravel(), yy.ravel()]
with dezero.no_grad():
score = model(X)
predict_cls = np.argmax(score.data, axis=1)
Z = predict_cls.reshape(xx.shape)
plt.contourf(xx, yy, Z)
# Plot data points of the dataset
N, CLS_NUM = 100, 3
markers = ['o', 'x', '^']
colors = ['orange', 'blue', 'green']
for i in range(len(x)):
c = t[i]
plt.scatter(x[i][0], x[i][1], s=40, marker=markers[c], c=colors[c])
plt.show()1. 하이퍼파라미서 설정
- '사람'이 결정하는 매개변수
- 은닉층 수와 학습률 등
- 에포크 300 : 준비된 데이터셋을 모두 사용했을 때 1에포크
- 배치 크기 30 : 데이터를 한 번에 30개씩 묶어 처리
2. 데이터셋을 읽고 모델과 옵티마이저 생성
* NOTE
- 여기에서 취급하는 데이터 총 300개
- 데이터가 많을 때는 모든 데이터를 한꺼번에 처리하는 대신 조금씩 무작위로 모아서 처리
- 미니배치 : 데이터 뭉치
3. np.random.permutation 함수로 데이터셋의 인덱스를 무작위로 섞음
- 인수로 N을 주면 0 ~ N-1까지 정수가 무작위로 배열된 리스트 반환
- 여기에서는 에포크 별로 indez = np.random.permutation(data_size)를 호출하여 무작위 정렬 색인 리스트 새로 생성
4. 미니배치 생성, 방금 생성한 index에서 앞에서부터 차례로 꺼내 사용
5. 기울기를 구하고 매개변수를 갱신
6. 에포크마다 손실 함수의 결과 출력


49. Dataset 클래스와 전처리
- Dataset 클래스는 기반 클래스로서의 역할
- 사용자가 실제로 사용하는 데이터셋은 이를 상속하여 구현하게 함
class Dataset:
def __init__(self, train=True, transform=None, target_transform=None):
self.train = train
self.transform = transform
self.target_transform = target_transform
if self.transform is None:
self.transform = lambda x: x
if self.target_transform is None:
self.target_transform = lambda x: x
self.data = None
self.label = None
self.prepare()
def __getitem__(self, index):
assert np.isscalar(index)
if self.label is None:
return self.transform(self.data[index]), None
else:
return self.transform(self.data[index]),\
self.target_transform(self.label[index])
def __len__(self):
return len(self.data)
def prepare(self):
pass- 초기화 때 train 인수 : 학습, 테스트를 구별하기 위함
- 인스턴스 변수 data와 label에 각각 입력 데이터와 레이블 보관
- 자식 클래스에서는 prepare 메서드가 데이터 준비 작업을 하도록 구현 - Dataset 클래스에서 중요한 메서드 __getitem__ & __len__
- __getitem__
- 파이썬 특수 메서드, x[0]이나 x[1]처럼 괄호를 사용해 접근할 때의 동작을 정의
- 단순히 지정된 인덱스에 위치하는 데이터를 꺼냄 - __len__ : len 함수를 사용할 때 호출
49.2 큰 데이터셋의 경우
- 작은 데이터셋은 Dataset 클래스의 인스턴스 변수인 data와 label에 직접 ndarray 인스턴스를 유지해도 무리 없음
- 큰 데이터셋에서는 이런 방식 활용할 수 없음
class BigData(Dataset):
def __getitem__(index):
x = np.load('data/{}.np', format(index))
t = np.load('label/{}.npy', format(index))
return x, t
def __len__():
return 1000000- BigData 클래스를 초기화할 때는 데이터를 아직 읽지 않고, 데이터에 접근할 때 비로소 읽게 하는 것
- 구체적으로 __getitem(index)가 불리는 시점에서 data 디렉터리에 있는 데이터를 읽음
49.3 데이터 이어 붙이기
신경망을 학습시킬 때는 데이터셋 중 일부를 미니배치로 꺼냄
train_set = dezero.datasets.Spiral()
batch_index = [0, 1, 2] # 0에서 2번째까지의 데이터를 꺼냄
batch = [train_set[i] for i in batch_index]
x = np.array([example[0] for example in batch])
t = np.array([example[1] for example in batch])
print(x.shape)
print(t.shape)
# 실행 결과
(3, 2)
(3, )- 인덱스를 지정하여 여러 데이터(미니배치)를 꺼냄
- batch에 여러 데이터가 리스트로 저장
49.4 학습 코드
if '__file__' in globals():
import os, sys
sys.path.append(os.path.join(os.path.dirname(__file__), '..'))
import math
import numpy as np
import dezero
import dezero.functions as F
from dezero import optimizers
from dezero.models import MLP
max_epoch = 300
batch_size = 30
hidden_size = 10
lr = 1.0
train_set = dezero.datasets.Spiral(train=True)
model = MLP((hidden_size, 3))
optimizer = optimizers.SGD(lr).setup(model)
data_size = len(train_set)
max_iter = math.ceil(data_size / batch_size)
for epoch in range(max_epoch):
# Shuffle index for data
index = np.random.permutation(data_size)
sum_loss = 0
for i in range(max_iter):
# Create minibatch
batch_index = index[i * batch_size:(i + 1) * batch_size]
batch = [train_set[i] for i in batch_index]
batch_x = np.array([example[0] for example in batch])
batch_t = np.array([example[1] for example in batch])
y = model(batch_x)
loss = F.softmax_cross_entropy(y, batch_t)
model.cleargrads()
loss.backward()
optimizer.update()
sum_loss += float(loss.data) * len(batch_t)
# Print loss every epoch
avg_loss = sum_loss / data_size
print('epoch %d, loss %.2f' % (epoch + 1, avg_loss))- Dataset 클래스를 사용하여 신경망 학습
49.5 데이터셋 전처리
데이터 확장
- 이미지를 회전 혹은 좌우 반전시키거나 데이터 수를 인위적으로 늘리는 기술(데이터 확장)도 자주 이용
- 이러한 전처리에 대응하기 위해 Dataset 클래스에도 전처리 기능 추가
전처리 기능 추가 코드
class Dataset:
def __init__(self, train=True, transform=None, target_transform=None):
self.train = train
self.transform = transform
self.target_transform = target_transform
if self.transform is None:
self.transform = lambda x: x
if self.target_transform is None:
self.target_transform = lambda x: x
self.data = None
self.label = None
self.prepare()
def __getitem__(self, index):
assert np.isscalar(index)
if self.label is None:
return self.transform(self.data[index]), None
else:
return self.transform(self.data[index]),\
self.target_transform(self.label[index])
def __len__(self):
return len(self.data)
def prepare(self):
pass- 초기화 시에 transform과 target_transform을 새롭게 받음
- transform : 입력 데이터 하나에 대한 변환 처리
- target_transform : 레이블 하나에 대한 변환 처리
def f(x):
y = x / 2.0
return y
train_set = dezero.datasets.Spiral(transform=f)- 입력 데이터를 1/2로 스케일 변환하는 전처리 예
- dezero/transform에 전처리 시 자주 사용되는 변환 저장(생략)
사용 예시
from dezero import transforms
f = transforms.Normalize(mean=0.0, std=2.0)
train_set = dezero.datasets.Spiral(transforms=f)
f = transforms.Compose([transforms.Normalize(mean=0.0, std=2.0),
transforms.AsType(np.gloat64)])- 여러 변환 처리를 연달아 수행할 수도 있음
50. 미니배치를 뽑아주는 DataLoader
'반복자'
DataLoader 클래스를 구현하는 흐름
50.1 반복자란
반복자(iterator) : 원소를 반복하여 꺼내줌
- 파이썬 반복자
: 리스트나 튜플 등 여러 원소를담고 있는 데이터 타입으로부터 데이터를 순차적으로 추출하는 기능 제공
t = [1, 2, 3]
x = iter(t)
next(x)
>>> 1
next(x)
>>> 2
next(x)
>>> 3
next9x)
>>> 에러- 리스트를 반복자로 변환하려면 iter 함수를 사용
- 리스트 t에서 x라는 반복자를 만듦
- 반복자에서 데이터를 순서대로 추출하기 위해 next 함수를 사용
- 원소가 더는 존재하지 않으면 StopIteration 예외 발생
* NOTE
- for문에서 리스트의 원소를 꺼낼 때 내부적으로 반복자가 이용됨
- t = [1, 2, 3]일 때 for x in t: x를 실행하면 리스트 t가 내부적으로 반복자로 변환
파이썬에서 반복자를 직접 만들 수도 있음
class MyIterator:
def __init(self, max_xnt):
self.max_cnt = max_cnt
self.cnt = 0
# 자기 자신을 반환
def __iter__(self):
return self
# 다음 원소를 반환
# 반환할 원소가 없다면 raise StopIteration()을 수행
def __next__(self):
if self.cnt == self.max_cnt:
raise StopIteration()
self.cnt += 1
return self.cnt
사용 코드
obj = MyIterator(5)
for x in obj :
print(x)
# 실행 결과
1
2
3
4
5- for x in obj: 구문으로 원소를 꺼낼 수 있음
미니배치를 뽑아주는 DataLoader 클래스 구현
import math
pil_available = True
try:
from PIL import Image
except:
pil_available = False
import numpy as np
from dezero import cuda
class DataLoader:
def __init__(self, dataset, batch_size, shuffle=True, gpu=False):
self.dataset = dataset
self.batch_size = batch_size
self.shuffle = shuffle
self.data_size = len(dataset)
self.max_iter = math.ceil(self.data_size / batch_size)
self.gpu = gpu
self.reset()
def reset(self):
self.iteration = 0
if self.shuffle:
self.index = np.random.permutation(len(self.dataset))
else:
self.index = np.arange(len(self.dataset))
def __iter__(self):
return self
def __next__(self):
if self.iteration >= self.max_iter:
self.reset()
raise StopIteration
i, batch_size = self.iteration, self.batch_size
batch_index = self.index[i * batch_size:(i + 1) * batch_size]
batch = [self.dataset[i] for i in batch_index]
xp = cuda.cupy if self.gpu else np
x = xp.array([example[0] for example in batch])
t = xp.array([example[1] for example in batch])
self.iteration += 1
return x, t
def next(self):
return self.__next__()- 데이터셋의 첫 데이터부터 차례로 꺼내줌
- 필요에 따라 뒤섞을 수 있음
초기화 메서드는 다음 인수를 받음
- dataset : Dataset 인터페이스를 만족하는 인스턴스
- batch_size : 배치 크기
- shuffle : 에포크별로 데이터셋을 뒤섞을지 여부
초기화 코드
- 인수를 인스턴스 변수로 저장한 후 reset 메서드를 부름
reset 메서드
- 인스턴스 변수의 반복 횟수를 0으로 설정하고 필요에 따라 데이터의 인덱스를 뒤섞음
__next__ 메서드
- 미니배치를 꺼내 ndarray 인스턴스로 변환
50.2 DataLoader 사용하기
미니배치를 꺼내오는 일이 간단해짐
train_set = Spiral(train=True)
test_set = Spiral(train=False)
train_loader = DataLoader(train_set, batch_size)
test_loader = DataLoader(test_set, batch_size, shuffle=False)
for epoch in range9max_epoch):
for x, t in train_loader:
print(x.shape, t.shape) # x, t는 훈련 데이터
break
# 에포크 끝에서 테스트 데이터를 꺼낸다
for x, t in test_loader:
print(x.shape, t.shape) # x, t는 테스트 데이터
break- 훈련용과 테스트용, 총 두 개의 DataLoader 생성
- 훈련용 : 에포크별로 데이터를 뒤섞어야 하므로 shuffle=True
- 테스트용 : 정확도 평가에만 사용하므로 shuffle=False - 미니배치 추출과 데이터 뒤섞기는 DataLoader가 알아서 해줌
50.3 accuracy 함수 구현하기
인식 정확도를 평가해주는 accuracy 함수
def accuracy(y, t):
y, t = as_variable(y), as_variable(t)
pred = y.data.argmax(axis=1).reshape(t.shape)
result = (pred == t.data)
acc = result.mean()
return Variable(as_array(acc))- y는 신경망의 예측 결과, t는 정답 데이터
- 신경망 예측 결과를 구해 pred에 저장
- 예측 결과의 최대 인덱스를 찾아서 형상을 변경
- pred와 정답 데이터 t를 비교하면 결과는 True/False의 텐서가 됨
- 텐서의 True 비율(평균)이 정답률
* CAUTION
- accuracy 함수는 Variable 인스턴스를 반환
- 내부 계산은 ndarray 인스턴스를 사용
50.4 스파이럴 데이터셋 학습 코드
DataLoader 클래스와 accuracy 함수를 사용하여 스파이럴 데이터셋 학습
max_epoch = 300
batch_size = 30
hidden_size = 10
lr = 1.0
train_set = dezero.datasets.Spiral(train=True)
test_set = dezero.datasets.Spiral(train=False)
train_loader = DataLoader(train_set, batch_size)
test_loader = DataLoader(test_set, batch_size, shuffle=False)
model = MLP((hidden_size, 3))
optimizer = optimizers.SGD(lr).setup(model)
for epoch in range(max_epoch):
sum_loss, sum_acc = 0, 0
for x, t in train_loader: # 1. 훈련용 미니배치 데이터
y = model(x)
loss = F.softmax_cross_entropy(y, t)
acc = F.accuracy(y, t) # 2. 훈련 데이터의 인식 정확도
model.cleargrads()
loss.backward()
optimizer.update()
sum_loss += float(loss.data) * len(t)
sum_acc += float(acc.data) * len(t)
print('epoch: {}'.format(epoch+1))
print('train loss: {:.4f}, accuracy: {:.4f}'.format(
sum_loss / len(train_set), sum_acc / len(train_set)))
sum_loss, sum_acc = 0, 0
with dezero.no_grad(): # 3. 기울기 불필요 모드
for x, t in test_loader: # 4. 테스트용 미니배치 데이터
y = model(x)
loss = F.softmax_cross_entropy(y, t)
acc = F.accuracy(y, t) # 5. 테스트 데이터의 인식 정확도
sum_loss += float(loss.data) * len(t)
sum_acc += float(acc.data) * len(t)
print('test loss: {:.4f}, accuracy: {:.4f}'.format(
sum_loss / len(test_set), sum_acc / len(test_set)))- DataLoader 사용해 미니배치 꺼냄
- accuracy 함수를 사용하여 인식 정확도 계산
- 에포크별로 테스트 데이터셋을 사용하여 훈련 결과를 평가
- 테스트 시에는 역전파가 필요 없으므로 with dezero.no_grad(): 블록 내부로 들어감
- 역전파 관련 처리와 자원 소모를 피할 수 있음 - 테스트용 DataLoader에서 미니배치 데이터를 꺼내 평가
- accuracy 함수를 사용하여 인식 정확도 계산

- 에포크가 진행됨에 따라 손실(loss)이 낮아지고 인식 정확도(accuracy)는 상승 = 학습이 제대로 이루어지고 있음
- 훈련(train)과 테스트(test)의 차이가 작은데, 모델이 과대적합을 일으키지 않았다는 뜻
* NOTE : 과대적합
- 특정 훈련 데이터에 지나치게 최적화된 상태
51. MNIST 학습
- Dataset 클래스 : 데이터셋 처리를 위한 공통 인터페이스 마련, '전처리' 설정
- DataLoader 클래스 : Dataset에서 미니배치 단위로 데이터 꺼내올 수 있게 함

- 전처리를 수행하는 계층은 호출 가능하다는 뜻에서 Callable로 표시
- Calable은 Dataset이 보유하고 Dataset은 DataLoader가 보유하는 관계
- 사용자는 DataLoader로부터 미니배치 가져옴
51.1 MNIST 데이터셋
51.2 MNIST 학습하기
51.3 모델 개선하기
- 이전 신경망의 활성화 함수는 시그모이드 함수
- 최근에는 ReLU라는 함수가 더 자주 사용
ReLU
- 입력이 0보다 크면 입력 그대로 출력, 0 이하면 0을 출력

class ReLU(Function):
def forward(self, x):
xp = cuda.get_array_module(x)
y = xp.maximum(x, 0.0) # 1
return y
def backward(self, gy):
x, = self.inputs
mask = x.data > 0 # 2
gx = gy * mask # 3
return gx
def relu(x):
return ReLU()(x)- np.maximum(x, 0, 0) : x의 원소와 0.0 중 큰 쪽을 반환
- 역전파에서는 입력 x에서 0보다 큰 원소에 해당하는 위치와 기울기는 그대로 흘려보내고, 0 이하라면 기울기를 0으로 설정 - 출력 쪽에서 전해지는 기울기를 '통과시킬지' 표시한 마스크(mask)를 준비한 후
- 기울기를 곱해줌
* CAUTION
- ReLU 함수가 하는 일은 신호를 '통과'시키거나 '봉쇄'하는 것
ReLU 함수를 사용하여 새로운 신경망
model = MLP((hidden_size, 10), activation=F.relu)
칼럼 : 딥러닝 프레임워크
딥러닝 프레임워크들은 성숙기에 접어들며 거의 같은 방향
- Define-by-Run 방식으로 게산 그래프를 만들 수 있음
- 사전 정의된 다양한 함수와 계층을 제공함
- 다양한 매개변수 갱신 클래스(옵티마이저)를 제공함
- 모델은 상속을 통해 구현할 수 있음
- 데이터셋을 관리하는 클래스를 제공함
- CPU 외에도 GPU나 특정한 ASIC도 활용할 수 있음
- 성능 향상을 위해(그리고 실제 제품에 적용할 것을 대비해) Define-and-Rum 모드 실행도 지원함
* NOTE
- 딥러닝 '프레임워크'는 '도구'나 '라이브러리'가 아님
- 라이브러리와 프레임워크의 차이는 프로그램을 '누가' 제어하느냐
- 라이브러리 : 편의 함수와 데이터 구조의 모음
- 사용자는 라이브러리에서 필요한 것을 적당히 꺼내 사용
- 프로그램 제어(코드를 어떤 순서로 실행할지)는 사용자가 정함 - 프레임워크 : 전체의 토대를 제공
- 딥러닝 프레임워크라면 자동 미분의 기초를 제공하고 사용자는 그 위에 필요한 계산을 구축
- 전체적인 제어 역할을 프레임워크가 담당 - 두 차이는 '누가' 제어하느냐에 차이가 있음

Define-by-Run 방식의 자동 미분
- 딥러닝 프레임워크에서 가장 중요한 기능 '자동 미분'
- 귀찮은 계산과 코드 작성 없이도 즉시 미분값을 계산할 수 있음
- 현대의 프레임워크는 계산 그래프를 Define-by-Run 방식으로 만들어줌
- 코드는 즉시 실행되고, 동시에 뒤편에서는 계산 그래프가 만들어지는 것
→ 우리는 파이썬 구문만 사용해서도 계산 그래프를 만들 수 있음
- 파이토치에서 텐서를 표현하는 클래스는 Tensor
- Define-by-Run : 즉시 계산이 수행되고 보이지 않는 곳에서 계산들의 '연결'이 만들어짐
- 미분값을 구하기 위해 y.backward()를 수행
- 파이토치, 체이너, 텐서플로는 Define-and-Run(정적 계산 그래프) 모드도 지원
- Define-by-Run : 시행착오를 많이 겪는 연구/개발 단계에 적합
- Define-and-Run : 성능이 요구되는 실제 제품(서비스)이나 IoT 기기 같은 에지 환경에서 사용할 때 적합
계층 컬렉션
- 신경망에서 사용하는 모델은 Linear 계층과 Sigmoid 계층 등 이미 준비된 계층들을 조합해 구축
- 레고블록처럼 조합하여 원하는 딥러닝 모델 구축
- 프레임워크가 유용한 계층 컬렉션을 제공해야 함
(ex. 체이너의 계층)

중요한 점 : 계층 컬렉션은 '자동 미분' 구조 위에 구축됨!

- 딥러닝 프레임워크의 밑동은 자동 미분 구조
- 자동 미분 구조를 이용하여 다양한 계층을 제공
옵티마이저 컬렉션
- 딥러닝 학습은 매개변수의 기울기를 사용하여 매개변수들을 하나씩 갱신
- 갱신 방법은 지금도 계속해서 제안되는 중
→ 별도의 모듈로 제공
이러한 모듈을 '옵티마이저'라고 부름

- 다양한 옵티마이저를 제공하여 사용자는 매개변수 갱신 작업을 높은 차원에서 생각할 수 있게 됨
- 다른 옵티마이저로 전환하기도 쉬워서 실험과 검증을 반복하기가 훨씬 쉽고 원활
정리

- 그림의 세 가지 요소는 거의 모든 프레임워크가 제공하는 중요한 기능
- 특히 자동 미분은 '기둥'
: 자동 미분 기능 위에 다양한 계층 컬렉션을 쌓아 올림으로써 프레임워크의 골격이 완성 - 매개변수 갱신용 옵티마이저 컬렉션을 제공함으로써 딥러닝에서 수행하는 작업의 대부분에 대응할 수 있게 됨
세 가지 핵심 기능의 구조를 이해하면 프레임워크를 큰 그림에서 더 단순하게 볼 수 있는 눈이 생김!
'AI > 딥러닝 프레임워크 기초' 카테고리의 다른 글
| [밑시딥③] 제5고지. DeZero의 도전(편) (2) | 2024.03.07 |
|---|---|
| [밑시딥③] 제5고지. DeZero의 도전(전편) (1) | 2024.03.06 |
| [밑시딥③] 제4고지. 신경망 만들기(전편) (1) | 2024.03.04 |
| [밑시딥③] 제3고지. 고차 미분 계산(후편) (1) | 2024.02.27 |
| [밑시딥③] 제3고지. 고차 미분 계산(전편) (1) | 2024.02.26 |
